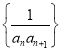题目内容
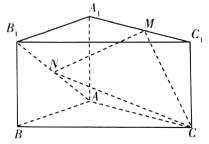
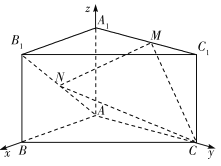
【题目】【2018海南高三阶段性测试(二模)】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一动点.
上一动点.
(I)是否存在一点![]() ,使得线段
,使得线段![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(II)若点![]() 为
为![]() 的中点且
的中点且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(I)见解析(II)![]()
【解析】试题分析:
(1)存在点![]() ,且
,且![]() 为
为![]() 的中点.连接
的中点.连接![]() ,
, ![]() ,由三角形中位线的性质可得
,由三角形中位线的性质可得![]() ,结合线面平行的判定定理可得
,结合线面平行的判定定理可得![]() 平面
平面![]() .
.
(2)由题意结合勾股定理可求得![]() .以点
.以点![]() 为坐标原点,
为坐标原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴建立空间直角坐标系,可得平面
轴建立空间直角坐标系,可得平面![]() 的一个法向量为
的一个法向量为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,据此计算可得二面角
,据此计算可得二面角![]() 的正弦值为
的正弦值为![]() .
.
试题解析:
(1)存在点![]() ,且
,且![]() 为
为![]() 的中点.证明如下:
的中点.证明如下:
如图,连接![]() ,
, ![]() ,点
,点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,
所以![]() 为
为![]() 的一条中位线,
的一条中位线, ![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
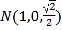
(2)设![]() ,则
,则![]() ,
, ![]()
![]()
![]()
![]() ,
,
![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() .
.
由题意以点![]() 为坐标原点,
为坐标原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴建立如图所示的空间直角坐标系,可得
轴建立如图所示的空间直角坐标系,可得![]() ,
, ![]() ,
, 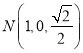 ,
, ![]() ,
,
故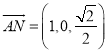 ,
, ![]() ,
, 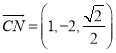 ,
, ![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
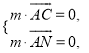 得
得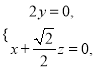
令![]() ,得平面
,得平面![]() 的一个法向量
的一个法向量![]() ,
,
同理可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
故二面角![]() 的余弦值为
的余弦值为![]()
![]() .
.
故二面角![]() 的正弦值为
的正弦值为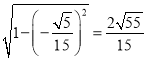 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】已知随机变量 ![]() 的取值为不大于
的取值为不大于 ![]() 的非负整数值,它的分布列为:
的非负整数值,它的分布列为:
| 0 | 1 | 2 |
| n |
|
|
|
|
|
|
其中 ![]() (
( ![]() )满足:
)满足: ![]() ,且
,且 ![]() .
.
定义由 ![]() 生成的函数
生成的函数 ![]() ,令
,令 ![]() .
.
(I)若由 ![]() 生成的函数
生成的函数 ![]() ,求
,求 ![]() 的值;
的值;
(II)求证:随机变量 ![]() 的数学期望
的数学期望 ![]() ,
, ![]() 的方差
的方差 ![]() ;
;
( ![]() )
)
(Ⅲ)现投掷一枚骰子两次,随机变量 ![]() 表示两次掷出的点数之和,此时由
表示两次掷出的点数之和,此时由 ![]() 生成的函数记为
生成的函数记为 ![]() ,求
,求 ![]() 的值.
的值.