题目内容
已知数列 的前
的前 项和为
项和为 记
记
(1)若数列 是首项与公差均为
是首项与公差均为 的等差数列,求
的等差数列,求 ;
;
(2)若 且数列
且数列 均是公比为
均是公比为 的等比数列,
的等比数列,
求证:对任意正整数 ,
,
【答案】
(1)0 (2)证明详见解析.
【解析】
试题分析:(1)根据等差数列的通项公式和前n项和公式,求出an,Sn,然后代入f(n)中,整理即可求解.
(2)根据等比数列的通项公式求出 的表达式,可得
的表达式,可得 ,再求出
,再求出 ,代入f(n)中,整理得
,代入f(n)中,整理得 ,然后证
,然后证
 0即可.
0即可.
试题解析:(1)  数列
数列 是首项与公差均为
是首项与公差均为 的等差数列, 1分
的等差数列, 1分


 3分
3分


 5分
5分
故 6分
6分
(2)由题意
 7分
7分
 8分
8分
故 9分
9分



 10分
10分
(证法一)当 时,
时, ; 11分
; 11分
当 时,
时, , 12分
, 12分
 13分
13分
故对任意正整数 ,
, 14分
14分
(证法二)




 11分
11分
 ,
,
 ,
,
数列 是递增数列. 12分
是递增数列. 12分
 13分
13分
 14分
14分
考点:1. 等差数列、等比数列的通项公式和前n项和公式;(2)不等式的证明.

练习册系列答案
相关题目
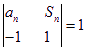 (
( 的前
的前 项和为
项和为 ,
, ,且
,且
 是等比数列;
是等比数列; 为数列
为数列 的前n项和,求
的前n项和,求 的值.
的值. 的前
的前 项和为
项和为 ,
, ,且
,且
 是等比数列;
是等比数列; 为数列
为数列 的前n项和,求
的前n项和,求 的值.
的值.