题目内容
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() (
(![]() 为正整数).
为正整数).
(1)求数列![]() 的通项公式;
的通项公式;
(2)记![]() ,若对任意正整数
,若对任意正整数![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围?
的取值范围?
(3)已知集合![]() ,若以a为首项,a为公比的等比数列前n项和记为
,若以a为首项,a为公比的等比数列前n项和记为![]() ,问是否存在实数a使得对于任意的
,问是否存在实数a使得对于任意的![]() .若存在,求出a的取值范围;若不存在,说明理由.
.若存在,求出a的取值范围;若不存在,说明理由.
(1) ![]() (2)
(2)![]() (3)存在
(3)存在![]()
解析:
(1) 由题意知,当![]() 时,
时, 两式相减变形得:
两式相减变形得:![]()
又![]() 时,
时, ![]() ,于是
,于是 ![]() ……………………1分
……………………1分
故 ![]() 是以
是以![]() 为首项,公比
为首项,公比![]() 的等比数列
的等比数列
![]() …………………………………4分
…………………………………4分
由 得
得 ![]() =
=![]() ……………5分
……………5分
当n是偶数时,![]() 是
是![]() 的增函数, 于是
的增函数, 于是![]() ,故
,故![]() ……………7分
……………7分
当n是奇数时,![]() 是
是![]() 的减函数, 因为
的减函数, 因为![]() ,故k≤1.………………9分
,故k≤1.………………9分
综上所述,k的取值范围是![]() …………………………………10分
…………………………………10分
(3)①当![]() ,
,
![]() ,若
,若![]()
 此不等式组的解集为空集.
此不等式组的解集为空集.
即当![]() a. ……………………………13分
a. ……………………………13分
②当![]()
而![]() 是关于n的增函数.
是关于n的增函数.
且![]() ……………………………15分
……………………………15分
因此对任意的![]() 要使
要使 解得
解得![]() ……………18分
……………18分

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 的前
的前 项和为
项和为 ,满足
,满足 .
. 为等比数列,并
为等比数列,并 求出
求出 ;
; ,求
,求 的最大项.
的最大项. }的前
}的前 项和为
项和为 ,且
,且 (
( );
); =3
=3 (
(


 ;
; }的通项公式
}的通项公式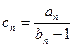 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且
,且 .
.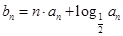 ,数列
,数列 的前
的前 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.