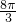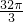Question

由曲线y=

x

和y=x³所围成的封闭图形的面积为（　　）

• A．

  1

  4

• B．

  5

  12

• C．

  2

  3

• D．

  11

  12

Answer 1

分析：作出两个曲线的图象，求出它们的交点，由此可得所求面积为函数

x

-x³在区间[0，1]上的定积分的值，再用定积分计算公式加以运算即可得到本题答案

解答：解：∵曲线y=x³和曲线y=

x

的交点为A（1，1）和原点O
∴曲线y=x³和曲线y=

x

所围图形的面积为
S=

∫

1 0

（

x

-x³）dx=（

2

3

x

3

2

-

1

4

x4）

|

1 0

=

2

3

-

1

4

=

5

12

故选：B

点评：本题求两条曲线围成的曲边图形的面积，着重考查了定积分的几何意义和积分计算公式等知识，属于基础题．