题目内容
把由曲线y=|x|和y=2围成的图形绕x轴旋转360°，所得旋转体的体积为（ ）A．
B．
C．
D．
【答案】分析：画出曲线y=|x|和y=2围成的图形，推得旋转体的形状，求出底面面积，再求体积．
解答：
解：由题意，y=|x|和y=2围成图中阴影部分的图形，
旋转体为一个圆柱挖去两个相同的共顶点的圆锥．
∵V圆柱=π•22•4=16π，
2V圆锥=2×π×22×2=
∴所求几何体体积为16π-
=
．
故选D．
点评：本题考查圆锥的结构特征，考查计算能力，作图能力，逻辑思维能力，是基础题．
解答：
解：由题意，y=|x|和y=2围成图中阴影部分的图形，旋转体为一个圆柱挖去两个相同的共顶点的圆锥．
∵V圆柱=π•22•4=16π，
2V圆锥=2×π×22×2=
∴所求几何体体积为16π-
=．故选D．
点评：本题考查圆锥的结构特征，考查计算能力，作图能力，逻辑思维能力，是基础题．
练习册系列答案
相关题目
把由曲线y=|x|和y=2围成的图形绕x轴旋转360°，所得旋转体的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
(x≥0)与半椭圆
合成的曲线称作“果圆”(其中a2＝b2＋c2，a＞b＞c＞0)．如图，设点F0，F1，F2是相应椭圆的焦点，A1、A2和B1、B2是“果圆”与x，y轴的交点，若△F0F1F2是边长为1的等边三角，则a，b的值分别为
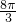
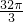
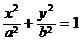(x≥0)与半椭圆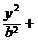
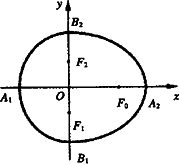
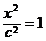(x≤0)合成的曲线称作“果圆”，其中a2=b2+c2，a>0,b>c>0，如图，点F0，F1，F2是相应椭圆的焦点，A1、A2和B1、B2分别是“果圆”与x 、y轴的交点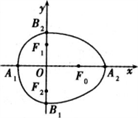
的取值范围．