题目内容
已知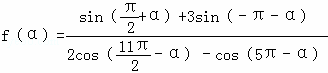 .
.
(1)化简f(α);
(2)已知tanα=3,求f(α)的值.
考点:
诱导公式的作用;同角三角函数间的基本关系.
专题:
三角函数的求值.
分析:
(1)利用诱导公式可得![]() =cosα,sin(﹣π﹣α)=sinα,
=cosα,sin(﹣π﹣α)=sinα,![]() =﹣sinα,cos(5π﹣α)=﹣cosα,进而化简化简f(α);
=﹣sinα,cos(5π﹣α)=﹣cosα,进而化简化简f(α);
(2)由tanα=3,将(1)中化简所得式子,分子分母同除以cosα(弦化切)后,代入可得答案.
解答:
解:(1)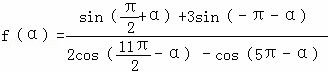 =
=![]()
(2)∵tanα=3
∴f(α)=![]() =
=![]() =
=![]() =﹣2
=﹣2
点评:
本题考查的知识点是诱导公式,同角三角函数间的基本关系,(1)的关键是理解“奇变偶不变,符号看象限“的原则,(2)的关键是掌握“弦化切“的技巧.

练习册系列答案
相关题目
 ,
, 的值.
的值. .
. ,求f(α)的值.
,求f(α)的值. .
. ,求f(α)的值.
,求f(α)的值. .
. ,求f(α)的值.
,求f(α)的值. .
.