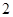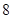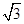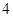题目内容
已知抛物线y2=2px(p≠0)及定点A(a,b),B(-a,0),ab≠0,b2≠2pa,M是抛物线上的点.设直线AM、BM与抛物线的另一个交点分别为M1、M2,当M变动时,直线M1M2恒过一个定点,此定点坐标为________.

设M ,M1
,M1 ,M2
,M2 ,
,
由点A、M、M1共线可知 =
= ,
,
得y1= ,同理由点B、M、M2共线得y2=
,同理由点B、M、M2共线得y2= .
.
设(x,y)是直线M1M2上的点,则 ,
,
即y1y2=y(y1+y2)-2px,又y1= ,y2=
,y2= ,
,
则(2px-by) +2pb·(a-x)y0+2pa·(by-2pa)=0.
+2pb·(a-x)y0+2pa·(by-2pa)=0.
当x=a,y= 时上式恒成立,即定点为
时上式恒成立,即定点为 .
.
 ,M1
,M1 ,M2
,M2 ,
,由点A、M、M1共线可知
 =
= ,
,得y1=
 ,同理由点B、M、M2共线得y2=
,同理由点B、M、M2共线得y2= .
.设(x,y)是直线M1M2上的点,则
 ,
,即y1y2=y(y1+y2)-2px,又y1=
 ,y2=
,y2= ,
,则(2px-by)
 +2pb·(a-x)y0+2pa·(by-2pa)=0.
+2pb·(a-x)y0+2pa·(by-2pa)=0.当x=a,y=
 时上式恒成立,即定点为
时上式恒成立,即定点为 .
.
练习册系列答案
相关题目
 ,求点A的坐标;
,求点A的坐标; 上的动点,点P在y轴上的射影是M,点A 的坐标是(4,a),则当
上的动点,点P在y轴上的射影是M,点A 的坐标是(4,a),则当 时,
时, 的最小值是( )
的最小值是( )



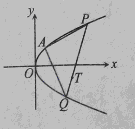
 的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且
的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且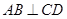 ,则
,则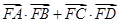 的最大等于 ( )
的最大等于 ( )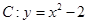 ,过原点的动直线
,过原点的动直线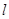 交抛物线
交抛物线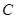 于
于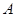 、
、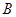 两点,
两点,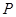 是
是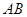 的中点,设动点
的中点,设动点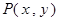 ,则
,则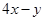 的最大值是( )
的最大值是( )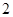
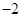
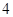
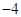
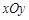 中,抛物线
中,抛物线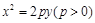 上纵坐标为
上纵坐标为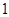 的点到焦点的距离
的点到焦点的距离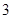 ,则焦点到准线的距离为( )
,则焦点到准线的距离为( )