题目内容
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() 且
且![]() .
.
(1)求证![]() 是等差数列,并求出
是等差数列,并求出![]() 的表达式;
的表达式;
(2) 若![]() ,求证
,求证![]()
(I)证明:∵![]()
∴当n≥2时,an = Sn – Sn – 1
又![]()
∴![]() ,
,
若Sn = 0,则an = 0,
∴a1 = 0与a1 =![]() 矛盾!
矛盾!
∴Sn≠0,Sn – 1≠0.
∴![]() 即
即![]()
又![]() .
.
∴{![]() }是首项为2,公差为2的等差数列 ……………..6分
}是首项为2,公差为2的等差数列 ……………..6分
(II)证明:由(I)知![]()
∴![]()
![]()
![]()
![]() ……..12分
……..12分

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,满足
,满足 .
. 为等比数列,并
为等比数列,并 求出
求出 ;
; ,求
,求 的最大项.
的最大项. }的前
}的前 项和为
项和为 ,且
,且 (
( );
); =3
=3 (
(


 ;
; }的通项公式
}的通项公式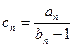 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且
,且 .
.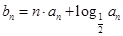 ,数列
,数列 的前
的前 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.