题目内容
自点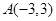 发出的光线
发出的光线 射到
射到 轴上,被
轴上,被 轴反射,其反射光线所在直线与圆
轴反射,其反射光线所在直线与圆 相切,求光线
相切,求光线 所在直线的方程。
所在直线的方程。
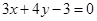 或
或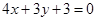 .
.
解析试题分析:已知圆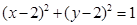 关于
关于 轴的对称圆
轴的对称圆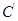 的方程为
的方程为 2分
2分
如图所示.
可设光线 所在直线方程为
所在直线方程为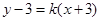 , 4分
, 4分
∵直线 与圆
与圆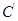 相切,
相切,
∴圆心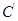
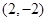 到直线
到直线 的距离
的距离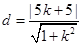 =
=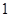 , 6分
, 6分
解得 或
或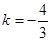 . 10分
. 10分
∴光线 所在直线的方程为
所在直线的方程为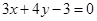 或
或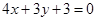 .…12分
.…12分
考点:点关于直线的对称点;直线与圆的位置关系;点到直线的距离公式。
点评:本题也可以这样做:求出点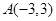 关于x轴的对称点
关于x轴的对称点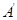 ,则反射光线一定过点
,则反射光线一定过点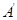 ,由此设出直线方程,利用直线与圆相切求出即可。在设直线方程的点斜式时,要注意讨论直线的斜率是否存在。
,由此设出直线方程,利用直线与圆相切求出即可。在设直线方程的点斜式时,要注意讨论直线的斜率是否存在。

练习册系列答案
相关题目
 .请将n表示为m的函数.
.请将n表示为m的函数. 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线 交圆C于A、B两点。
交圆C于A、B两点。 时,写出直线
时,写出直线 .
. )向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标. 截圆心在点
截圆心在点 的圆
的圆 所得弦长为
所得弦长为 .
.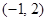 的圆
的圆
 |PD|.
|PD|.
 :
: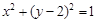 ,设点
,设点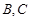 是直线
是直线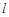 :
: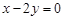 上的两点,它们的横坐标分别
上的两点,它们的横坐标分别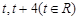 ,
,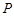 点的纵坐标为
点的纵坐标为 且点
且点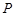 在线段
在线段 上,过
上,过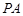 ,切点为
,切点为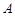
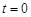 ,
,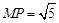 ,求直线
,求直线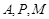 三点的圆的圆心是
三点的圆的圆心是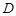 ,
,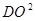 表示成
表示成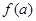 ,并写出定义域.
,并写出定义域.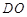 长的最小值
长的最小值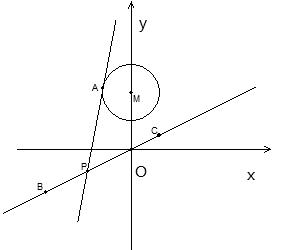
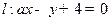 及圆
及圆
 ,求a的值.
,求a的值.