题目内容
在数列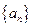 中,
中,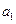 ,
,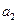 是给定的非零整数,
是给定的非零整数,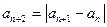 .
.
(1)若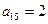 ,
,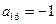 ,求
,求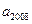 ;(2)证明:从
;(2)证明:从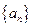 中一定可以选取无穷多项组成两个不同的常数数列.
中一定可以选取无穷多项组成两个不同的常数数列.
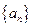 中,
中,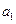 ,
,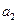 是给定的非零整数,
是给定的非零整数,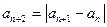 .
.(1)若
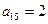 ,
,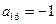 ,求
,求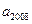 ;(2)证明:从
;(2)证明:从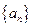 中一定可以选取无穷多项组成两个不同的常数数列.
中一定可以选取无穷多项组成两个不同的常数数列.(1)1 (2)略
(1)∵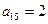 ,
,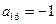 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,……
,……
∴自第22项起,每三个相邻的项周期地取值1,1,0,故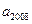 =1.……4分
=1.……4分
(2)首先证明数列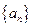 必在有限项后出现零项.假设
必在有限项后出现零项.假设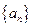 中没有零项,
中没有零项,
由于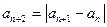 ,所以.
,所以. 时,都有
时,都有 .……………………6分
.……………………6分
当 时,
时, (
( );
);
当 时,
时, (
( ),
),
即 的值要么比
的值要么比 至少小1,要么比
至少小1,要么比 至少小1.…………………8分
至少小1.…………………8分
令 ,
, ,则
,则 .
.
由于 是确定的正整数,这样下去,必然存在某项
是确定的正整数,这样下去,必然存在某项 ,这与
,这与 矛盾,从而
矛盾,从而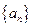 中必有零项.……………………………………………10分
中必有零项.……………………………………………10分
若第一次出现的零项为 ,记
,记 ,则自第
,则自第 项开始,每三个相邻的项周期地取值
项开始,每三个相邻的项周期地取值 ,即
,即 ,
,
所以数列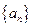 中一定可以选取无穷多项组成两个不同的常数数列.……12分
中一定可以选取无穷多项组成两个不同的常数数列.……12分
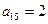 ,
,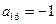 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,……
,……∴自第22项起,每三个相邻的项周期地取值1,1,0,故
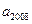 =1.……4分
=1.……4分(2)首先证明数列
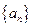 必在有限项后出现零项.假设
必在有限项后出现零项.假设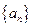 中没有零项,
中没有零项,由于
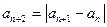 ,所以.
,所以. 时,都有
时,都有 .……………………6分
.……………………6分当
 时,
时, (
( );
);当
 时,
时, (
( ),
),即
 的值要么比
的值要么比 至少小1,要么比
至少小1,要么比 至少小1.…………………8分
至少小1.…………………8分令
 ,
, ,则
,则 .
.由于
 是确定的正整数,这样下去,必然存在某项
是确定的正整数,这样下去,必然存在某项 ,这与
,这与 矛盾,从而
矛盾,从而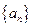 中必有零项.……………………………………………10分
中必有零项.……………………………………………10分若第一次出现的零项为
 ,记
,记 ,则自第
,则自第 项开始,每三个相邻的项周期地取值
项开始,每三个相邻的项周期地取值 ,即
,即 ,
,
所以数列
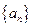 中一定可以选取无穷多项组成两个不同的常数数列.……12分
中一定可以选取无穷多项组成两个不同的常数数列.……12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
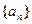 的首项为
的首项为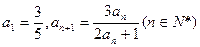 (1)若
(1)若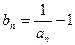 ,求证:数列
,求证:数列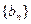 是等比数列;(2)若
是等比数列;(2)若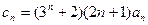 ,求数列
,求数列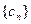 的前
的前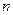 项和.
项和.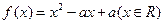 同时满足:①不等式
同时满足:①不等式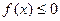 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在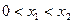 ,使得不等式
,使得不等式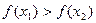 成立。设数列
成立。设数列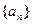 的前n项和
的前n项和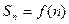 。(1)求
。(1)求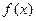 的解析式;(2)求数列
的解析式;(2)求数列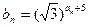 ,
,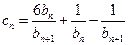 ,
,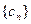 前n项和为
前n项和为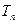 ,
,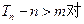 (
(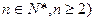 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.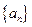 中,
中,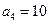 且
且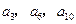 成等比数列,求数列
成等比数列,求数列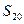 .
.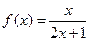 ,数列
,数列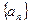 满足
满足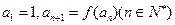 .
.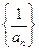 是等差数列;(Ⅱ)记
是等差数列;(Ⅱ)记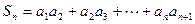 ,试比较
,试比较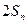 与1的大小.
与1的大小.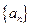 的前项和为
的前项和为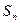 ,且
,且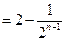 ,
,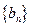 为等差数列,且
为等差数列,且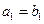 ,
,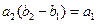 .
.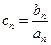 ,求数列
,求数列 的前
的前 项和
项和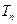 .
.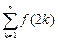 = 。
= 。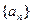 是等差数列,则( )
是等差数列,则( )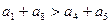 B
B 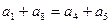
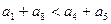 D
D 