题目内容
若(ax+2b)6的展开式中x3与x4的系数之比为4:3,其中a>0,b≠0
(1)当a=1时,求(ax+2b)6的展开式中二项式系数最大的项;
(2)令F(a,b)=
,求F(a,b)的最小值.
(1)当a=1时,求(ax+2b)6的展开式中二项式系数最大的项;
(2)令F(a,b)=
| b3+16 |
| a |
(1)(ax+2b)6的展开式中含x3的项为
(ax)3(2b)3,
故其系数为8
a3b3=160a3b3,
含x4的项为
(ax)4(2b)2,系数为4
a4b2=60a4b2,
故可得
=
,解得a=2b,
所以当a=1时,(ax+2b)6=(x+1)6展开式中二项式系数最大的项为:
T4=
x3=20x3
(2)由a=2b>0,F(a,b)=
=
+
,
构造函数F(x)=
+
,x>0
求导数可得F′(x)=x-
,
令F′(x)>0,可解得x>2,令F′(x)<0,可解得0<x<2,
故函数F(x)在(0,2)单调递减,在(2,+∞)单调递增,
故可得F(a,b)的最小值为F(2)=6
| C | 36 |
故其系数为8
| C | 36 |
含x4的项为
| C | 46 |
| C | 46 |
故可得
| 160a3b3 |
| 60a4b2 |
| 4 |
| 3 |
所以当a=1时,(ax+2b)6=(x+1)6展开式中二项式系数最大的项为:
T4=
| C | 36 |
(2)由a=2b>0,F(a,b)=
| b3+16 |
| a |
| b2 |
| 2 |
| 8 |
| b |
构造函数F(x)=
| x2 |
| 2 |
| 8 |
| x |
求导数可得F′(x)=x-
| 8 |
| x2 |
令F′(x)>0,可解得x>2,令F′(x)<0,可解得0<x<2,
故函数F(x)在(0,2)单调递减,在(2,+∞)单调递增,
故可得F(a,b)的最小值为F(2)=6

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

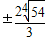
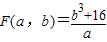 ,求F(a,b)的最小值.
,求F(a,b)的最小值.