题目内容
（本题满分14分）已知函数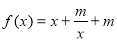
（
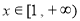且
）.
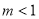（Ⅰ）用定义证明函数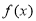
在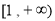
上为增函数；
（Ⅱ）设函数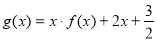
，若[2, 5 ]是
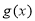的一个单调区间，且在该区间上
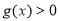恒成立，求实数m的取值范围.
【解析】
试题分析：（Ⅰ）设
（
）（
）
∵
, 
∴
＜0, 
＞0
∴
∴函数
在
上为增函数
（Ⅱ）
对称轴
，定义域x∈[2, 5]
①
在[2, 5]上单调递增且
②
在[2, 5]上单调递减且
无解
综上所述
考点：本题考查用定义证明单调性，以及二次函数恒成立问题
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
作圆
的两条切线，切点分别为A、B，则直线AB的方程为
B．
D．
已知函数
的图像是连续不断的，有如下的
对应值表：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 123．5 | 21．5 | －7．82 | 11．57 | －53．7 | －126．7 | －129．6 |
那么函数
在区间
上的零点至少有（ ）
A．2个 B．3个 C．4个 D．5个
的解集是全体实数的条件是（ ）
B．
C．
D．
的三个内角
的对边分别是
，且
， 则角
等于（ ）
B 
或
C 
D 
，
，
.
；
,求实数
的取值范围．
的解集是 .
的右顶点为A，上顶点为B，点M为线段AB的靠近点B的三等分点，
MOA=45°，则椭圆的离心率为 .
（
）的离心率是 ；渐近线方程是 ．