题目内容
11．在等比数列{an}中，a1=1，a4=8，则数列{an}的前5项和是（ ）| A． | $\frac{85}{2}$ | B． | 32 | C． | 64 | D． | 31 |
分析 利用等比数列的通项公式与求和公式即可得出．
解答 解：设等比数列{an}的公比为q，∵a1=1，a4=8，∴q3=8，解得q=2．
则数列{an}的前5项和=$\frac{{2}^{5}-1}{2-1}$=31．
故选：D．
点评 本题考查了等比数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
1．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\sqrt{5}$，|$\overrightarrow{c}$|=1，若（$\overrightarrow{a}$-$\overrightarrow{c}$）•（$\overrightarrow{b}$-$\overrightarrow{c}$）=0，则|$\overrightarrow{a}$-$\overrightarrow{b}$|的取值范围是（ ）
| A． | [1，2] | B． | [2，4] | C． | [$\sqrt{7}$-1，$\sqrt{7}$+1] | D． | [$\sqrt{5}$-1，$\sqrt{5}$+1] |
2．某公司的组织结构图如图所示，其中技术服务部的直接领导是（ ）
| A． | 董事长 | B． | 监事会 | C． | 总经理 | D． | 总工程师 |
19．已知函数$f（x）=\left\{\begin{array}{l}（{4a-3}）x+2a-4，x≤t\\ 2{x^3}-6x，x＞t\end{array}\right.$，无论t取何值，函数f（x）在R上总是不单调，则实数a的取值范围是（ ）
| A． | （-∞，1） | B． | $[{\frac{1}{4}，+∞}）$ | C． | $[{\frac{3}{4}，+∞}）$ | D． | $（{-∞，\frac{3}{4}}]$ |
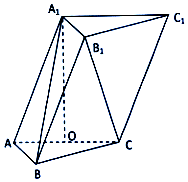如图，在三棱柱ABC-A1B1C1中，$AB=BC=\sqrt{5}，AC=2$且点A1在底面ABC上的射影O恰是线段AC的中点，$A{A_1}=\sqrt{5}$．
如图 已知四边形 ABCD 为直角梯形，AB⊥AD，DC∥AB，且边 AB、AD、DC 的长分别为 7cm，4cm，4cm，分别以 AB、AD、DC 三边所在直线为旋转轴，求所得几何体体积．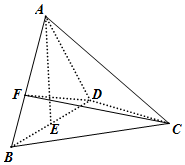
如图，在三棱锥A-BCD中，已知△ABD，△BCD都是边长为2的等边三角形，E为BD中点，且AE⊥平面BCD，F为线段AB上一动点，记$\frac{BF}{BA}=λ$．
1．已知e是自然对数的底数，函数f（x）=（ax2+x）ex，若f（x）在[-1，1]上是单调增函数，则a的取值范围是（ ）
| A． | [-$\frac{2}{3}$，0] | B． | （-∞，0）∪[$\frac{2}{3}$，+∞） | C． | [0，$\frac{2}{3}$] | D． | （-∞，-$\frac{2}{3}$]∪[0，+∞） |