题目内容
四棱锥P-ABCD的底面是边长为a的正方形,PA⊥平面ABCD,侧棱PB与底面ABCD所成的角为60°,则这个四棱锥的体积是
a3
a3.
| ||
| 3 |
| ||
| 3 |
分析:利用线面垂直和线面角即可得出四棱锥的高PA,再利用四棱锥的体积计算公式即可得出.
解答:解:如图所示,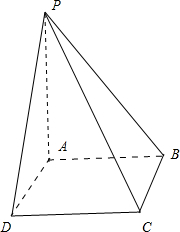
∵PA⊥平面ABCD,∴PA⊥AB,∴∠PBA=60°.
又AB=a,∴PA=AB•tan60°=
a.
∴VP-ABCD=
PA•S正方形ABCD
=
×
a•a2
=
a3.
故答案为
a3.

∵PA⊥平面ABCD,∴PA⊥AB,∴∠PBA=60°.
又AB=a,∴PA=AB•tan60°=
| 3 |
∴VP-ABCD=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 3 |
=
| ||
| 3 |
故答案为
| ||
| 3 |
点评:熟练掌握线面垂直的性质、线面角、四棱锥的体积计算公式等是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
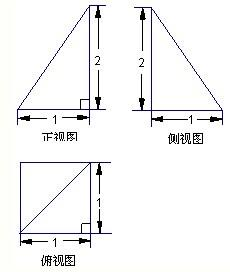 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
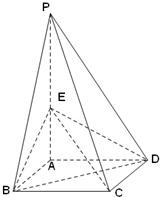 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: