题目内容
抛物线y=x2到直线x-y-2=0的最短距离为
- A.
- B.
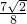
- C.
- D.以上都不对
B
分析：抛物线上设点P（x，y），从而可求点P到直线x-y-2=0的距离为
，进而利用配方法可求得
，由此可知抛物线y=x2到直线x-y-2=0的最短距离．
解答：抛物线上设点P（x，y），则
点P到直线x-y-2=0的距离为
∵点P（x，y）在抛物线y=x2上
∴y=x2，
∴
∴当
时，
即抛物线y=x2到直线x-y-2=0的最短距离为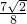
故选B．
点评：本题重点考查点到直线的距离，解题的关键是正确运用点到直线的距离，运用配方法求最短距离．
分析：抛物线上设点P（x，y），从而可求点P到直线x-y-2=0的距离为
，进而利用配方法可求得，由此可知抛物线y=x2到直线x-y-2=0的最短距离．解答：抛物线上设点P（x，y），则
点P到直线x-y-2=0的距离为
∵点P（x，y）在抛物线y=x2上
∴y=x2，
∴
∴当
时，即抛物线y=x2到直线x-y-2=0的最短距离为
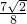
故选B．
点评：本题重点考查点到直线的距离，解题的关键是正确运用点到直线的距离，运用配方法求最短距离．
练习册系列答案
名校课堂系列答案
相关题目
抛物线y=x2到直线2x-y=4距离最近的点的坐标是（ ）
A、（
| ||||
| B、（1，1） | ||||
C、（
| ||||
| D、（2，4） |
，
）
，
）
，
）
，
）