题目内容
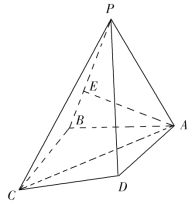
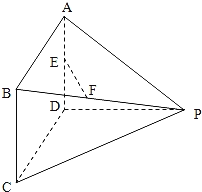
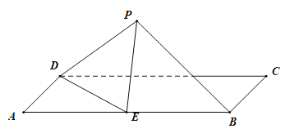
【题目】如图,平面![]()
![]() 平面
平面![]() ,
,![]() 为矩形,
为矩形,![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() .
.
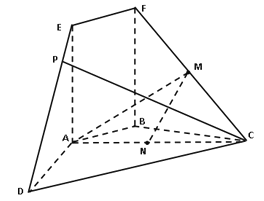
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在求出
,若存在求出![]() 的长,若不存在,说明理由.
的长,若不存在,说明理由.
【答案】(1)详见解析;(2)![]() ;(3)不存在这样的
;(3)不存在这样的![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)连接![]() ,利用三角形中位线性质可得
,利用三角形中位线性质可得![]() ,进而可证
,进而可证![]() 平面
平面![]() ;
;
(2)建立空间坐标系,求出两个平面的法向量,利用向量夹角公式及平方关系可得二面角![]() 的正弦值;
的正弦值;
(3)假设存在点![]() ,根据
,根据![]() 表示出点
表示出点![]() 的坐标,利用
的坐标,利用![]() 得出矛盾,进而得到结论.
得出矛盾,进而得到结论.
(1)连接![]() ,∵
,∵![]() ,
,![]() 为
为![]() ,
,![]() 中点,
中点,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() ,
,![]() ,
,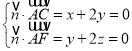 ,
,
令![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() .
.
设平面![]() 的一个方向量为
的一个方向量为![]() ,
,
∴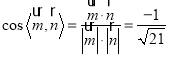 ,
,![]() ,
,
二面角![]() 的正弦值为
的正弦值为![]() .
.
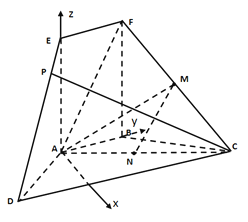
(3)假设存在这样一点![]() ,设
,设![]() ,由(2)知
,由(2)知![]() ,
,![]() ,平面
,平面![]() 的法向量
的法向量![]() .
.
设![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,
![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴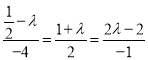 ,
,
∴![]() ,且
,且![]() ,即不存在这样的
,即不存在这样的![]() ,
,
∴线段![]() 上不存在点
上不存在点![]() ,使得
,使得![]() 平面
平面![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本![]() (元)与生产该产品的数量
(元)与生产该产品的数量![]() (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根据以上数据,绘制了散点图.观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型![]() 和指数函数模型
和指数函数模型![]() 分别对两个变量的关系进行拟合,已求得:用指数函数模型拟合的回归方程为
分别对两个变量的关系进行拟合,已求得:用指数函数模型拟合的回归方程为![]() ,
,![]() 与
与![]() 的相关系数
的相关系数![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(其中
,(其中![]() );
);
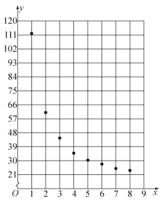
(1)用反比例函数模型求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本.
参考数据:![]() ,
,![]()
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: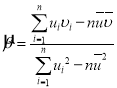 ,
,![]() ,相关系数
,相关系数 .
.
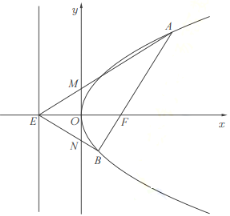
【题目】如图,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 的焦点为
的焦点为![]() ,准线与
,准线与![]() 轴的交点为
轴的交点为![]() .过点
.过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 、
、![]() 两点,
两点,![]() 、
、![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,当
两点,当![]() 轴时,
轴时,![]() .
.
(1)求抛物线的方程;
(2)设![]() 的面积为
的面积为![]() ,
,![]() 面积为
面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
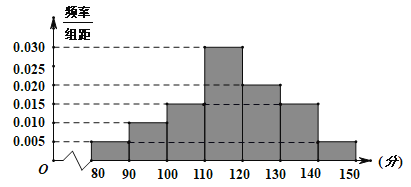
【题目】某健身机构统计了去年该机构所有消费者的消费金额(单位:元),如下图所示:

(1)将去年的消费金额超过 3200 元的消费者称为“健身达人”,现从所有“健身达人”中随机抽取 2 人,求至少有 1 位消费者,其去年的消费金额超过 4000 元的概率;
(2)针对这些消费者,该健身机构今年欲实施入会制,详情如下表:
会员等级 | 消费金额 |
普通会员 | 2000 |
银卡会员 | 2700 |
金卡会员 | 3200 |
预计去年消费金额在![]() 内的消费者今年都将会申请办理普通会员,消费金额在
内的消费者今年都将会申请办理普通会员,消费金额在![]() 内的消费者都将会申请办理银卡会员,消费金额在
内的消费者都将会申请办理银卡会员,消费金额在![]() 内的消费者都将会申请办理金卡会员. 消费者在申请办理会员时,需-次性缴清相应等级的消费金额.该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:
内的消费者都将会申请办理金卡会员. 消费者在申请办理会员时,需-次性缴清相应等级的消费金额.该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:
方案 1:按分层抽样从普通会员, 银卡会员, 金卡会员中总共抽取 25 位“幸运之星”给予奖励: 普通会员中的“幸运之星”每人奖励 500 元; 银卡会员中的“幸运之星”每人奖励 600 元; 金卡会员中的“幸运之星”每人奖励 800 元.
方案 2:每位会员均可参加摸奖游戏,游戏规则如下:从-个装有 3 个白球、 2 个红球(球只有颜色不同)的箱子中, 有放回地摸三次球,每次只能摸-个球.若摸到红球的总数消费金额/元为 2,则可获得 200 元奖励金; 若摸到红球的总数为 3,则可获得 300 元奖励金;其他情况不给予奖励. 规定每位普通会员均可参加 1 次摸奖游戏;每位银卡会员均可参加 2 次摸奖游戏;每位金卡会员均可参加 3 次摸奖游戏(每次摸奖的结果相互独立) .
以方案 2 的奖励金的数学期望为依据,请你预测哪-种方案投资较少?并说明理由.