题目内容
【题目】某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本![]() (元)与生产该产品的数量
(元)与生产该产品的数量![]() (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:
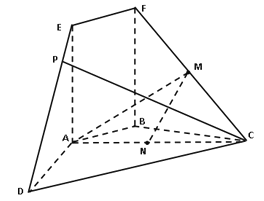
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根据以上数据,绘制了散点图.观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型![]() 和指数函数模型
和指数函数模型![]() 分别对两个变量的关系进行拟合,已求得:用指数函数模型拟合的回归方程为
分别对两个变量的关系进行拟合,已求得:用指数函数模型拟合的回归方程为![]() ,
,![]() 与
与![]() 的相关系数
的相关系数![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(其中
,(其中![]() );
);
(1)用反比例函数模型求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本.
参考数据:![]() ,
,![]()
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: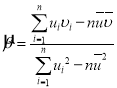 ,
,![]() ,相关系数
,相关系数 .
.
【答案】(1)![]() (2)用反比例函数模型拟合效果更好;当产量为10千件时,每件产品的非原料成本估计为21元
(2)用反比例函数模型拟合效果更好;当产量为10千件时,每件产品的非原料成本估计为21元
【解析】
(1)令![]() ,则
,则![]() 可转化为
可转化为![]() ,分别求出
,分别求出![]() 和
和![]() ,即求得回归方程;
,即求得回归方程;
(2)直接利用相关系数公式求![]() 与
与![]() 的相关系数,可得
的相关系数,可得![]() ,得到用反比例函数模型拟合效果更好,取
,得到用反比例函数模型拟合效果更好,取![]() ,可得当产量为10千件时,每件产品的非原料成本为21元.
,可得当产量为10千件时,每件产品的非原料成本为21元.
(1)令![]() ,则
,则![]() 可转化为
可转化为![]() ,
,
因为![]() ,所以
,所以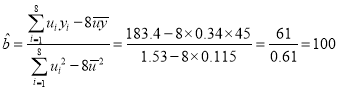
则![]() ,所以
,所以![]() ,
,
所以![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ;
;
(2)![]() 与
与![]() 的相关系数为:
的相关系数为:
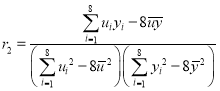
![]()
因为![]() ,所以用反比例函数模型拟合效果更好,
,所以用反比例函数模型拟合效果更好,
把![]() 代入回归方程:
代入回归方程:![]() ,
,![]() (元)
(元)
所以当产量为10千件时,每件产品的非原料成本估计为21元.

【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,在高三年级中随机选取![]() 名学生进行跟踪问卷,其中每周线上学习数学时间不少于
名学生进行跟踪问卷,其中每周线上学习数学时间不少于![]() 小时的有
小时的有![]() 人,在这
人,在这![]() 人中分数不足
人中分数不足![]() 分的有
分的有![]() 人;在每周线上学习数学时间不足于
人;在每周线上学习数学时间不足于![]() 小时的人中,在检测考试中数学平均成绩不足
小时的人中,在检测考试中数学平均成绩不足![]() 分的占
分的占![]() .
.
(1)请完成![]() 列联表;并判断是否有
列联表;并判断是否有![]() 的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
分数不少于 | 分数不足 | 合计 | |
线上学习时间不少于 | |||
线上学习时间不足 | |||
合计 |
(2)在上述样本中从分数不足于![]() 分的学生中,按照分层抽样的方法,抽到线上学习时间不少于
分的学生中,按照分层抽样的方法,抽到线上学习时间不少于![]() 小时和线上学习时间不足
小时和线上学习时间不足![]() 小时的学生共
小时的学生共![]() 名,若在这
名,若在这![]() 名学生中随机抽取
名学生中随机抽取![]() 人,求这
人,求这![]() 人每周线上学习时间都不足
人每周线上学习时间都不足![]() 小时的概率.(临界值表仅供参考)
小时的概率.(临界值表仅供参考)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式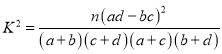 ,其中
,其中![]() )
)