题目内容
设 是A的对立事件,
是A的对立事件, 是B的对立事件。若和事件A+B发生的概率为0.4,则积事件
是B的对立事件。若和事件A+B发生的概率为0.4,则积事件 ·
· 发生的概率为( )
发生的概率为( )
| A.0.24 | B.0.36 | C.0.4 | D.0.6 |
D
解析试题分析:根据和事件与积事件的意义,分析易得和事件A+B与积事件 互为对立事件,由对立事件的概率性质,可得答案.解:根据题意,和事件A+B为A、B两个事件至少有一个发生,而积事件
互为对立事件,由对立事件的概率性质,可得答案.解:根据题意,和事件A+B为A、B两个事件至少有一个发生,而积事件 为A、B两个事件都不发生;分析易得和事件A+B与积事件互为对立事件;则积事件
为A、B两个事件都不发生;分析易得和事件A+B与积事件互为对立事件;则积事件 发生的概率为1-0.4=0.6;故选D
发生的概率为1-0.4=0.6;故选D
考点:对立事件的概率
点评:本题考查对立事件的概率性质,难点在于发现和事件A+B与积事件 互为对立事件.
互为对立事件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
随机变量X服从二项分布X~ ,且
,且 则
则 等于 ( )
等于 ( )
A. | B.0 | C.1 | D. |
随机变量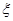 服从二项分布
服从二项分布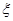 ~
~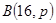 ,且
,且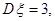 则
则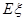 等于( )
等于( )
| A.4 | B.12 | C.4或12 | D.3 |
设随机变量 的分布列为
的分布列为 ,则
,则 ()
()
A. | B. | C. | D. |
下图是正态分布N(0,1)的正态曲线图,下面3个式子中,等于图中阴影部分面积的个数为( )。注:Φ P
P

① ②
②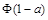 ③
③
| A.0 | B.1 | C.2 | D.3 |
如图所示,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96颗,以此实验数据为依据可以估计出椭圆的面积约为( ) 
| A.8.68 | B.16.32 | C.17.32 | D.7.68 |
在区间 上任取2个数
上任取2个数 ,若向量
,若向量 ,则
,则 的概率是
的概率是
A. | B.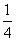 |
C. | D. |
若在区域 内任取一点P,则点P恰好在单位圆
内任取一点P,则点P恰好在单位圆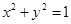 内的概率为( )
内的概率为( )
A. | B. | C. | D. |




