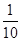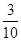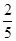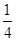题目内容
在区间
上任取2个数
，若向量
，则
的概率是
A． | B． |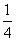
C． | D． |
D
解析试题分析：由,得
，又
，
，故的概率为
.
考点：几何概型
点评：本题考查等可能事件的概率，是一个几何概型，几何概型的概率的值是通过长度、面积、和体积、的比值得到结果，是一个基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知一个样本的方差为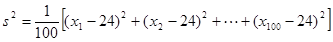
，
若这个样本的容量为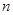
，平均数为
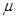，则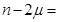
( )
| A．0 | B．24 | C．52 | D．148 |
设
是A的对立事件，
是B的对立事件。若和事件A+B发生的概率为0．4，则积事件·发生的概率为（ ）
| A．0．24 | B．0．36 | C．0．4 | D．0．6 |
米的绳子，拉直后在任意位置剪断，则剪得两段的长度都不小于1米，且以剪得的两段绳为两边的矩形的面积都不大于
平方米的概率为（ ）
某人射击一次击中的概率为0．6，经过3次射击，此人恰有两次击中目标的概率为（ ）
A． | B． | C． | D． |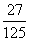
某小组有3名男生和2名女生，从中任选2名同学参加演讲比赛，那么互斥不对立的两个事件是
| A．恰有1名男生与恰有2名女生 |
| B．至少有1名男生与全是男生 |
| C．至少有1名男生与至少有1名女生 |
| D．至少有1名男生与全是女生 |
从装有2个黑球和2个白球的口袋内任取2个球，那么互斥而对立的两个事件是（ ）
| A．至少有1个黑球，至少有1个白球 | B．恰有1个黑球，恰有2个白球 |
| C．至少有1个黑球，都是黑球 | D．至少有1个黑球，都是白球 |
从装有
个红球和个黒球的口袋内任取个球，那么互斥而不对立的两个事件是
| A．至少有一个黒球与都是红球 | B．至少有一个黒球与都是黒球 |
C．至少有一个黒球与至少有 个红球 | D．恰有个黒球与恰有个黒球 |