题目内容
如图所示,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96颗,以此实验数据为依据可以估计出椭圆的面积约为( ) 
| A.8.68 | B.16.32 | C.17.32 | D.7.68 |
B
解析试题分析:欲估计出椭圆的面积,可利用概率模拟,只要利用平面图形的面积比求出落在椭圆外的概率即可.解:∵黄豆落在椭圆外的概率为:(矩形面积-椭圆面积):矩形面积= 故选B.
故选B.
考点:几何概型
点评:本题考查几何概型.如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,称为几何概型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若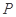 为
为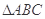 内一点,且
内一点,且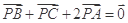 ,在
,在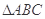 内随机撒一颗豆子,则此豆子落在
内随机撒一颗豆子,则此豆子落在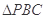 内的概率为( )
内的概率为( )
A.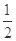 | B.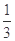 | C.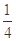 | D.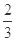 |
设 是A的对立事件,
是A的对立事件, 是B的对立事件。若和事件A+B发生的概率为0.4,则积事件
是B的对立事件。若和事件A+B发生的概率为0.4,则积事件 ·
· 发生的概率为( )
发生的概率为( )
| A.0.24 | B.0.36 | C.0.4 | D.0.6 |
右表是一个 列联表,则表中
列联表,则表中 处的值分别为
处的值分别为
| A.94 96 | B.52 50 |
| C.52 60 | D.54 52 |
某人射击一次击中的概率为0.6,经过3次射击,此人恰有两次击中目标的概率为( )
A. | B. | C. | D.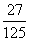 |
从装有2个黑球和2个白球的口袋内任取2个球,那么互斥而对立的两个事件是( )
| A.至少有1个黑球,至少有1个白球 | B.恰有1个黑球,恰有2个白球 |
| C.至少有1个黑球,都是黑球 | D.至少有1个黑球,都是白球 |
从三件正品、一件次品中随机取出两件,则取出的产品全是正品的概率是
A. | B. | C.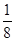 | D.无法确定 |
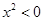 ”是不可能事件
”是不可能事件 米的绳子,拉直后在任意位置剪断,则剪得两段的长度都不小于1米,且以剪得的两段绳为两边的矩形的面积都不大于
米的绳子,拉直后在任意位置剪断,则剪得两段的长度都不小于1米,且以剪得的两段绳为两边的矩形的面积都不大于 平方米的概率为( )
平方米的概率为( )


