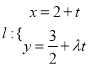题目内容
【题目】已知矩形![]() 的长
的长![]() ,宽
,宽![]() ,将其沿对角线
,将其沿对角线![]() 折起,得到四面体
折起,得到四面体![]() ,
,
如图所示,给出下列结论:
①四面体![]() 体积的最大值为
体积的最大值为![]() ;
;
②四面体![]() 外接球的表面积恒为定值;
外接球的表面积恒为定值;
③若![]() 分别为棱
分别为棱![]() 的中点,则恒有
的中点,则恒有![]() 且
且![]() ;
;
④当二面角![]() 为直二面角时,直线
为直二面角时,直线![]() 所成角的余弦值为
所成角的余弦值为![]() ;
;
⑤当二面角![]() 的大小为
的大小为![]() 时,棱
时,棱![]() 的长为
的长为![]() .
.
其中正确的结论有____________________(请写出所有正确结论的序号)
【答案】②③④
【解析】![]()
对于①四面体![]() 体积最大为两个面互相垂直,四面体
体积最大为两个面互相垂直,四面体![]() 体积的最大值为
体积的最大值为![]() ,故不正确;②三棱锥
,故不正确;②三棱锥![]() 外接球的半径为
外接球的半径为![]() ,所以三棱锥
,所以三棱锥![]() 外接球的表面积为
外接球的表面积为![]() ,②正确;③若
,②正确;③若![]() 为分别棱
为分别棱![]() 的中点,连接
的中点,连接![]() ,则
,则![]() ,根据等腰三角形三线合一得到
,根据等腰三角形三线合一得到![]() ,连接
,连接![]() ,容易判断
,容易判断![]() ,得到
,得到![]() ,所以
,所以![]() ,所以③正确;④二面角
,所以③正确;④二面角![]() 为直二面角时,以
为直二面角时,以![]() 为原点
为原点![]() 所在直线分别为
所在直线分别为![]() 轴,则由向量的数量积可以得到直线
轴,则由向量的数量积可以得到直线![]() 所成角的余弦值为
所成角的余弦值为![]() ,所以④正确;
,所以④正确;
⑤当二面角![]() 的大小为
的大小为![]() 时,棱
时,棱![]() 的长为
的长为![]() ,在直角三角形
,在直角三角形![]() 中,
中,
![]() ,作
,作![]() ,则
,则![]() ,同理直角三角形
,同理直角三角形![]() 中,则
中,则![]() ,在平面
,在平面![]() 内,过
内,过![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,易得四边形
,易得四边形![]() 为矩形,则
为矩形,则![]() ,又
,又![]() ,即有
,即有![]() 为二面角
为二面角![]() 的平面角,且为
的平面角,且为![]() ,即
,即![]() ,由
,由![]() 平面
平面![]() ,得到
,得到![]() ,即有
,即有![]() ,则
,则![]() ,故⑤错误,故答案为②③④.
,故⑤错误,故答案为②③④.

练习册系列答案
相关题目
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下表所示:
零件的个数x/个 | 2 | 3 | 4 | 5 |
加工的时间y/h | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
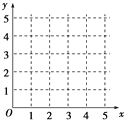
(2)求出y关于x的线性回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间.