Question

【题目】选修4-4：坐标系与参数方程

在平面直角坐标系中， 的参数方程为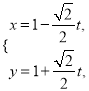（为参数），在以坐标原点为极点， 轴正半轴为极轴的极坐标系中， 的极坐标方程.

（Ⅰ）说明是哪种曲线，并将的方程化为普通方程；

（Ⅱ）与有两个公共点，顶点的极坐标，求线段的长及定点到两点的距离之积.

Answer 1

【答案】（Ⅰ）是圆， （Ⅱ）， .

【解析】试题分析：（Ⅰ）利用将极坐标方程化为直角坐标方程： （Ⅱ）利用直线参数方程几何意义得， ，将直线参数方程代入圆方程，利用韦达定理求解可得结果

试题解析：（Ⅰ） 是圆， 的极坐标方程，

化为普通方程： 即： ．

（Ⅱ）的极坐标平面直角坐标为在直线上，

将的参数方程为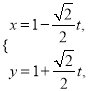（为参数）代入中得：

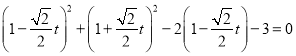化简得：

．设两根分别为，

由韦达定理知：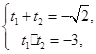

所以的长，

定点到两点的距离之积．