题目内容
10.在直角坐标系xOy中,曲线C的参数方程为$\left\{\begin{array}{l}{x=1+\sqrt{2}cosα}\\{y=1+\sqrt{2}sinα}\end{array}\right.$(α为参数),以坐标原点O为极点,以x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程是ρcos(θ-$\frac{π}{4}$)=$\sqrt{2}$.(1)写出曲线C的普通方程,直线l的直角坐标方程;
(2)设P为曲线C上任意一点,直线l和曲线C交于A,B两点,求|PA|2+|PB|2+|PO|2的取值范围.
分析 (1)由$\left\{\begin{array}{l}{x=1+\sqrt{2}cosα}\\{y=1+\sqrt{2}sinα}\end{array}\right.$得$\left\{\begin{array}{l}{x-1=\sqrt{2}cosθ}\\{y-1=\sqrt{2}sinθ}\end{array}\right.$,平方作和即可得到圆的普通方程;由ρcos(θ-$\frac{π}{4}$)=$\sqrt{2}$展开两角差的余弦,结合x=ρcosθ,y=ρsinθ求得直线l的直角坐标方程;
(2)直线方程和圆的方程解得A(2,0),B(0,2),设P($1+\sqrt{2}cosα,1+\sqrt{2}sinα$),代入|PA|2+|PB|2+|PO|2,得到|PA|2+|PB|2+|PO|2 =$12+4sin(α+\frac{π}{4})$,则|PA|2+|PB|2+|PO|2的取值范围可求.
解答 解:(1)由$\left\{\begin{array}{l}{x=1+\sqrt{2}cosα}\\{y=1+\sqrt{2}sinα}\end{array}\right.$(α为参数),得$\left\{\begin{array}{l}{x-1=\sqrt{2}cosθ}\\{y-1=\sqrt{2}sinθ}\end{array}\right.$,
平方作和得:(x-1)2+(y-1)2=2;
由ρcos(θ-$\frac{π}{4}$)=$\sqrt{2}$,得$ρcosθcos\frac{π}{4}+ρsinθsin\frac{π}{4}=\sqrt{2}$,
即$\frac{\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}y=\sqrt{2}$,x+y-2=0;
(2)联立$\left\{\begin{array}{l}{x+y-2=0}\\{(x-1)^{2}+(y-1)^{2}=2}\end{array}\right.$,解得A(2,0),B(0,2),
又O(0,0),设P($1+\sqrt{2}cosα,1+\sqrt{2}sinα$),
则|PA|2+|PB|2+|PO|2
=$(1+\sqrt{2}cosα)^{2}+(1+\sqrt{2}sinα)^{2}$+$(\sqrt{2}cosα-1)^{2}+(1+\sqrt{2}sinα)^{2}$+$(1+\sqrt{2}cosα)^{2}+(\sqrt{2}sinα-1)^{2}$
=$12+2\sqrt{2}(sinα+cosα)$=$12+4sin(α+\frac{π}{4})$.
∴|PA|2+|PB|2+|PO|2的最小值为8,最大值为16.
即|PA|2+|PB|2+|PO|2的取值范围是[8,16].
点评 本题考查了参数方程化普通方程,考查了极坐标方程化直角坐标方程,训练了参数方程在求解最值中的运用,是中档题.

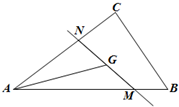 如图,直线MN过△ABC的重心G(重心是三角形三条中线的交点),设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),则mn的最小值是( )
如图,直线MN过△ABC的重心G(重心是三角形三条中线的交点),设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),则mn的最小值是( )| A. | $\frac{2}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{3}$ |
| A. | 1、0.、0.8 | B. | 0.6、0.8、1 | C. | 0.6、1、0.8 | D. | 0.6、0.6、0.8 |
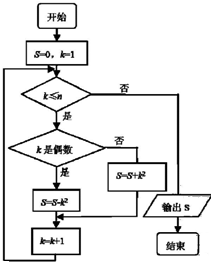 阅读如图所示的程序框图,运行相应的程序,若输入n的值为100,则输出S的值为( )
阅读如图所示的程序框图,运行相应的程序,若输入n的值为100,则输出S的值为( )| A. | -1050 | B. | 5050 | C. | -5050 | D. | -4950 |
 如图,圆O中AB=4为直径,直线CE与圆O相切于点C,AD⊥CE于点D,若AD=1,∠ACD=θ,则cosθ=$\frac{\sqrt{3}}{2}$.
如图,圆O中AB=4为直径,直线CE与圆O相切于点C,AD⊥CE于点D,若AD=1,∠ACD=θ,则cosθ=$\frac{\sqrt{3}}{2}$.