题目内容
1.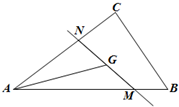 如图,直线MN过△ABC的重心G(重心是三角形三条中线的交点),设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),则mn的最小值是( )
如图,直线MN过△ABC的重心G(重心是三角形三条中线的交点),设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),则mn的最小值是( )| A. | $\frac{2}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{3}$ |
分析 由G为三角形的重心得到$\overrightarrow{AG}$=$\frac{1}{3}$($\overrightarrow{AB}+\overrightarrow{AC}$),再结合$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),根据M,G,N三点共线,易得到m,n的关系式,即可得到结论
解答 解:根据题意G为三角形的重心,
∴$\overrightarrow{AG}$=$\frac{1}{3}$($\overrightarrow{AB}+\overrightarrow{AC}$),
由于$\overrightarrow{MG}=\overrightarrow{AG}-\overrightarrow{AM}$=$\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})-m\overrightarrow{AB}$=($\frac{1}{3}$-m)$\overrightarrow{a}$+$\frac{1}{3}\overrightarrow{b}$,
$\overrightarrow{GN}=\overrightarrow{AN}-\overrightarrow{AG}$=n$\overrightarrow{b}$$-\frac{1}{3}(\overrightarrow{a}+\overrightarrow{b})$=$-\frac{1}{3}\overrightarrow{a}+(n-\frac{1}{3})\overrightarrow{b}$,
因为G,M,N三点共线,根据共线向量基本定理知,存在实数λ,使得$\overrightarrow{MG}=λ\overrightarrow{GN}$,
即$\left\{\begin{array}{l}{\frac{1}{3}-m=-\frac{1}{3}λ}\\{\frac{1}{3}=λ(n-\frac{1}{3})}\end{array}\right.$,
消去λ得m+n-3mn=0,m,n>0
∴m+n=3mn≥2$\sqrt{mn}$,所以mn≥$\frac{4}{9}$.所以mn的最小值为$\frac{4}{9}$;
故选:C.
点评 本题主要考查了三角形重心的性质,以及向量的基本定理和向量在几何中的应用,属于中档题

 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案| A. | f(x)=x${\;}^{\frac{1}{2}}$ | B. | f(x)=x3 | C. | f(x)=($\frac{1}{2}$)x | D. | f(x)=3x |
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
| A. | 0 | B. | ±2 | C. | 2 | D. | -2 |
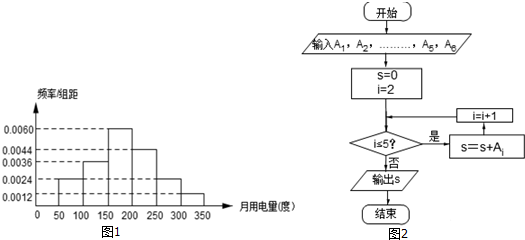
| A. | 820 | B. | 720 | C. | 620 | D. | 520 |
| A. | 1 | B. | -1 | C. | i | D. | -i |
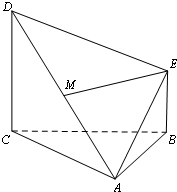 如图,多面体ABCDE中,CD⊥平面ABC,BE⊥平面ABC,AB=BC,BE=$\frac{1}{2}$CD,
如图,多面体ABCDE中,CD⊥平面ABC,BE⊥平面ABC,AB=BC,BE=$\frac{1}{2}$CD,