题目内容
已知：点
平面
，求证：过
有且只有一个平面
．
证明见答案
解析:
在平面
内任作两条相交直线
和
，则由
知
，
．点
和直线可确定一个平面
，点和直线可确定一个平面
．在平面，内过分别作直线
，
，故
，
是两条相交直线，可确定一个平面
．
，
，，
．
同理
，
又
，
，
，
．
所以过点有一个平面
．
假设过点还有一个平面
．
则在平面内取一直线
，
，点、直线确定一个平面
，由公理
知：
，
，
，
，
又
，
，
这与过一点有且只有一条直线与已知直线平行相矛盾，因此假设不成立，所以平面只有一个．
所以过平面外一点有且只有一个平面与已知平面平行．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
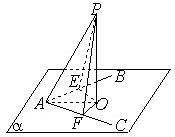如图，已知∠BAC在平面α内，P∉α，∠PAB=∠PAC，求证：点P在平面α上的射影在∠BAC的平分线上．
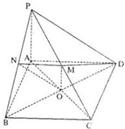如图，四棱锥P-ABCD的底面ABCD是边长为2的菱形，∠ABC=60°，点M是棱PC的中点，PA⊥平面ABCD，AC、BD交于点O．
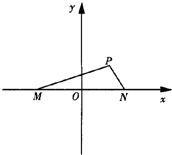如图，已知在坐标平面内，M、N是x轴上关于原点O对称的两点，P是上半平面内一点，△PMN的面积为
，直线
.求证：点P到直线
的距离