题目内容
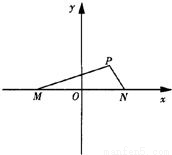
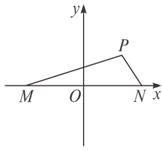
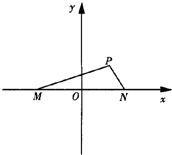 如图,已知在坐标平面内,M、N是x轴上关于原点O对称的两点,P是上半平面内一点,△PMN的面积为
如图,已知在坐标平面内,M、N是x轴上关于原点O对称的两点,P是上半平面内一点,△PMN的面积为| 3 |
| 2 |
| 3 |
| ||
| 2 |
| MP |
| OA |
| MN |
| OP |
| MN |
(Ⅰ)求以M、N为焦点且过点P的椭圆方程;
(Ⅱ)过点B(-1,0)的直线l交椭圆于C、D两点,交直线x=-4于点E,点B、E分
| CD |
分析:(Ⅰ)设M(-c,0),N(c,0)(c>0),P(x0,y0),则
•
=(2c,0)•(x0,y0)=2cx0,2cx0=2c,故x0=1.S△PMN=
(2c)|y0|=
,y0=
.
=(x0+c,y0),
=(1+
,
),由
=m=
,故
(x0+c)=(1+
)y0.由此入手能求出椭圆方程.
(Ⅱ)当l的斜率不存在时,l与x=-4无交点,不合题意.当l的斜率存在时,设l方程为y=k(x+1),代入椭圆方程
+y2=1,化简得:(4k2+1)x2+8k2x+4k2-4=0.设点C(x1,y1)、D(x2,y2),再由根的判别式和韦达定理进行求解.
| MN |
| OP |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2c |
| MP |
| OA |
| 3 |
| ||
| 2 |
| x0+c | ||
1+
|
| y0 | ||||
|
| ||
| 2 |
| 3 |
(Ⅱ)当l的斜率不存在时,l与x=-4无交点,不合题意.当l的斜率存在时,设l方程为y=k(x+1),代入椭圆方程
| x2 |
| 4 |
解答: 解:(Ⅰ)设M(-c,0),N(c,0)(c>0),P(x0,y0),
解:(Ⅰ)设M(-c,0),N(c,0)(c>0),P(x0,y0),
则
•
=(2c,0)•(x0,y0)=2cx0,2cx0=2c,故x0=1.①
又∵S△PMN=
(2c)|y0|=
,y0=
.②
∵
=(x0+c,y0),
=(1+
,
),
由已知(x0+c,y0)=m(1+
,
),
即
=m=
,故
(x0+c)=(1+
)y0.③
将①②代入③,
(1+c)=(1+
)•
,c2+c-(3+
)=0,(c-
)(c+
+1)=0,
∴c=
,y0=
.
设椭圆方程为
+
=1(a>b>0).
∵a2=b2+3,P(1,
)在椭圆上,
∴
+
=1,故b2=1,a2=4,
∴椭圆方程为:
+y2=1.
(Ⅱ)①当l的斜率不存在时,l与x=-4无交点,
不合题意.
②当l的斜率存在时,设l方程为y=k(x+1),
代入椭圆方程
+y2=1
化简得:(4k2+1)x2+8k2x+4k2-4=0.设点C(x1,y1)、D(x2,y2),
则:
,
∵-1=
,-4=
,
∴λ1=
,λ2=
,
λ1+λ2=-(
+
)=
[2x1x2+5(x1+x2)+8]
而2x1x2+5(x1+x2)+8=2•
+5•
+8=
(8k2-8-40k2+32k2+8)=0,
∴λ1+λ2=0.
 解:(Ⅰ)设M(-c,0),N(c,0)(c>0),P(x0,y0),
解:(Ⅰ)设M(-c,0),N(c,0)(c>0),P(x0,y0),则
| MN |
| OP |
又∵S△PMN=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2c |
∵
| MP |
| OA |
| 3 |
| ||
| 2 |
由已知(x0+c,y0)=m(1+
| 3 |
| ||
| 2 |
即
| x0+c | ||
1+
|
| y0 | ||||
|
| ||
| 2 |
| 3 |
将①②代入③,
| ||
| 2 |
| 3 |
| 3 |
| 2c |
| 3 |
| 3 |
| 3 |
∴c=
| 3 |
| ||
| 2 |
设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
∵a2=b2+3,P(1,
| ||
| 2 |
∴
| 1 |
| b2+3 |
| ||
| b2 |
∴椭圆方程为:
| x2 |
| 4 |
(Ⅱ)①当l的斜率不存在时,l与x=-4无交点,
不合题意.
②当l的斜率存在时,设l方程为y=k(x+1),
代入椭圆方程
| x2 |
| 4 |
化简得:(4k2+1)x2+8k2x+4k2-4=0.设点C(x1,y1)、D(x2,y2),
则:
|
∵-1=
| x1+λ1x2 |
| 1+λ1 |
| x1+λ2x2 |
| 1+λ2 |
∴λ1=
| -1-x1 |
| x2+1 |
| -4-x1 |
| x2+4 |
λ1+λ2=-(
| x1+1 |
| x2+1 |
| x1+4 |
| x2+4 |
| -1 |
| (x2+1)(x2+4) |
而2x1x2+5(x1+x2)+8=2•
| 4k2-4 |
| 4k2+1 |
| -8k2 |
| 4k2+1 |
| 1 |
| 4k2+1 |
∴λ1+λ2=0.
点评:本题考查椭圆方程的求法和求证λ1+λ2=0.解题时要认真审题,注意挖掘题设中的隐含条件,合理地运用椭圆的性质,恰当地进行等价转化.

练习册系列答案
相关题目
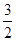 ,点A的坐标为(1+
,点A的坐标为(1+ ),
),  =m·
=m·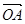 (m为常数),
(m为常数),



 的比分别为λ1、λ2,求λ1+λ2的值。
的比分别为λ1、λ2,求λ1+λ2的值。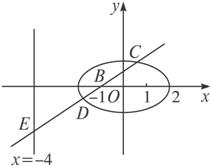
 PMN的面积为
PMN的面积为 ,点A的坐标为(1+
,点A的坐标为(1+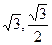 ),
), 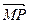 =m·
=m·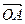 (m为常数),
(m为常数),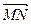
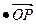

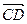 的比分别为λ1、λ2,求λ1+λ2的值。
的比分别为λ1、λ2,求λ1+λ2的值。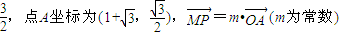 ,
,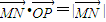 .
.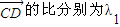 、λ2,求证:λ1+λ2=0.
、λ2,求证:λ1+λ2=0.