题目内容
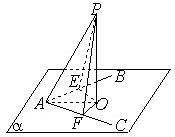 如图,已知∠BAC在平面α内,P∉α,∠PAB=∠PAC,求证:点P在平面α上的射影在∠BAC的平分线上.
如图,已知∠BAC在平面α内,P∉α,∠PAB=∠PAC,求证:点P在平面α上的射影在∠BAC的平分线上.
分析:作PO⊥α,PE⊥AB,PF⊥AC,垂足分别为O,E,F,连接OE,OF,OA,证明Rt△AOE≌Rt△AOF,然后得到点P在平面α上的射影在∠BAC的平分线上.
解答: 证明:作PO⊥α,PE⊥AB,PF⊥AC,
证明:作PO⊥α,PE⊥AB,PF⊥AC,
垂足分别为O,E,F,连接OE,OF,OA,
∵
?Rt△PAE≌Rt△PAF?AE=AF,
∵
?AB⊥PO,
又∵AB⊥PE,PO∩PE=P,
∴AB⊥平面PEO,
∴AB⊥OE,同理AC⊥OF.
在Rt△AOE和Rt△AOF,AE=AF,OA=OA,
∴Rt△AOE≌Rt△AOF,∴∠EAO=∠FAO,
即点P在平面α上的射影在∠BAC的平分线上.
 证明:作PO⊥α,PE⊥AB,PF⊥AC,
证明:作PO⊥α,PE⊥AB,PF⊥AC,垂足分别为O,E,F,连接OE,OF,OA,
∵
|
∵
|
又∵AB⊥PE,PO∩PE=P,
∴AB⊥平面PEO,
∴AB⊥OE,同理AC⊥OF.
在Rt△AOE和Rt△AOF,AE=AF,OA=OA,
∴Rt△AOE≌Rt△AOF,∴∠EAO=∠FAO,
即点P在平面α上的射影在∠BAC的平分线上.
点评:本题考查三垂线定理,考查学生逻辑思维能力,是基础题.

练习册系列答案
相关题目
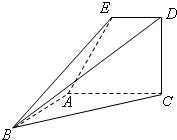 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.

