��Ŀ����
8�� һС��A�Ӿ�ֹ��ʼ��2m/s2�ļ��ٶ����ȼ��ٶ�ֱ���˶�������5���Ӻ������ٶ�Ϊ0������ֱ���˶���������10�룬�����-1m/s2�ļ��ٶ����ȼ��ٶ�ֱ���˶�ֱ��С����ֹ������һС��B��ͬһ��㣬�ӿ�ʼʱ�����ٶ�v0������ֱ���˶���
һС��A�Ӿ�ֹ��ʼ��2m/s2�ļ��ٶ����ȼ��ٶ�ֱ���˶�������5���Ӻ������ٶ�Ϊ0������ֱ���˶���������10�룬�����-1m/s2�ļ��ٶ����ȼ��ٶ�ֱ���˶�ֱ��С����ֹ������һС��B��ͬһ��㣬�ӿ�ʼʱ�����ٶ�v0������ֱ���˶�����1��д��С��A���ٶ�v��ʱ��t�ĺ�����ϵʽ���������亯��ͼ��
��2��д��С��A��λ��S��ʱ��t�ĺ�����ϵʽ��
��3����С��B��С��A�ľ�ֹ�ص���A��������С��B���ٶ�v0��������һ����ʱ�̣�
��4����С��A��B��������������ʱ�̣���С��B���ٶ�v0�ķ�Χ��
���� ��1��С��A�����ȼ����˶���5s���������˶����������˶����ٶȼ�Ϊ�ȼ����˶���ĩ�ٶȣ�����v=at��⣻
��2��ֱ����������ѧ֪ʶд��С��A��λ��S��ʱ��t�ĺ�����ϵʽ��
��3����С��B��С��A�ľ�ֹ�ص���A���������÷�����⣬������С��B���ٶ�v0��������һ����ʱ�̣��ж�����λ����⼴�ɣ�
��4��С��A��B��������������ʱ�̣����ö��η���������ʵ������������С��B���ٶ�v0�ķ�Χ��
���  �⣺��1�������⣬С��A�����ȼ����˶���0��t��5��v=2t��
�⣺��1�������⣬С��A�����ȼ����˶���0��t��5��v=2t��
5��t��15�������˶���v=10��
15��t��25���ȼ����˶���v=10-��t-15��=25-t��
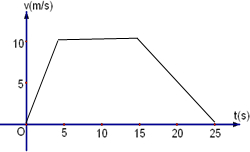
��v=$\left\{\begin{array}{l}{2t��0��t��5}\\{10��5��t��15}\\{25-t��15��t��25}\end{array}\right.$��
����ͼ����ͼ��ʾ����
��2��S=$\left\{\begin{array}{l}{t}^{2}��0��t��5\\ 10t-25��5��t��15\\ 25t-\frac{1}{2}{t}^{2}-\frac{275}{2}��15��t��25\end{array}\right.$��
��3��С��B��С��A�ľ�ֹ�ص���A������С��A��λ��Ϊ��25+100+50=175��
��B��25v0=175�����v0=7��
������һ����ʱ��Ϊt����Ȼǰ5�룬С��B��ǰ��С��A�ں�
��7t=25+10��t-5�������t=$\frac{25}{3}$��
��4����������г���������С��B������С��ֹͣǰ����������
��֪v0��7�������ڵ���ʱ�������������
v0t=$25t-\frac{1}{2}{t}^{2}-\frac{275}{2}$��15��t��25��
�ɵ�$25t-\frac{1}{2}{t}^{2}-\frac{275}{2}-{v}_{0}t=0$��$��25-{v}_{0}��^{2}-275��0$��
���v0��25-5$\sqrt{11}$��
С��B���ٶ�v0�ķ�Χ��[7��25-5$\sqrt{11}$��
���� ������Ҫ�������ȱ���ֱ���˶�������ʽ��ֱ��Ӧ�ã�Ҫ��ͬѧ���ܸ���������˶���������ٶ�-ʱ��ͼ���Ѷ����У�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | ��$\frac{��}{3}$��0�� | B�� | ��$\frac{��}{6}$��0�� | C�� | ��-$\frac{��}{3}$��0�� | D�� | ��-$\frac{��}{6}$��0�� |
| A�� | $\frac{kn}{m}$ | B�� | $\frac{km}{n}$ | C�� | k+m-n | D�� | k+m+n |
| A�� | �����ֵ������Сֵ | B�� | �����ֵ����Сֵ | ||
| C�� | ����Сֵ�������ֵ | D�� | ����ֵ |
| A�� | ��?x��R��ʹ|x|��0�� | B�� | ��?x��R��ʹ|x|��0�� | C�� | ��?x∉R��ʹ|x|��0�� | D�� | ��?x��R��ʹ|x|��0�� |
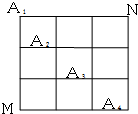 ��ͼ����ij�����У�M��N����֮��������ķ����ε�·����A1��A2��A3��A4�ǵ�·����λ��һ���Խ����ϵ�4�����㴦������ɵ�·��M�����������ѡ��һ���ؽֵ����·������N����
��ͼ����ij�����У�M��N����֮��������ķ����ε�·����A1��A2��A3��A4�ǵ�·����λ��һ���Խ����ϵ�4�����㴦������ɵ�·��M�����������ѡ��һ���ؽֵ����·������N����