题目内容
曲线y=1+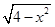 与直线y=k(x-2)+4有两个交点,则实数k的取值范围是( )
与直线y=k(x-2)+4有两个交点,则实数k的取值范围是( )
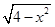 与直线y=k(x-2)+4有两个交点,则实数k的取值范围是( )
与直线y=k(x-2)+4有两个交点,则实数k的取值范围是( )A.(0, ) ) | B.( ,+∞) ,+∞) |
C.( , , ] ] | D.( , , ] ] |
D
试题分析:曲线y=1+
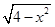 可以化为
可以化为 ,它表示以
,它表示以 为圆心,以
为圆心,以 为半径的圆的上半部分,而直线y=k(x-2)+4过定点
为半径的圆的上半部分,而直线y=k(x-2)+4过定点 ,画出图象可知当直线过点
,画出图象可知当直线过点 时,直线与半圆有两个交点,此时直线的斜率为
时,直线与半圆有两个交点,此时直线的斜率为 ;当直线与半圆相切时,直线斜率为
;当直线与半圆相切时,直线斜率为 ,所以要使半圆与曲线有两个交点,实数k的取值范围是(
,所以要使半圆与曲线有两个交点,实数k的取值范围是( ,
, ].
].点评:曲线曲线y=1+
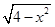 表示半圆,而不是一个完整的圆,解决此类问题一定要画出图形,数形结合解决.
表示半圆,而不是一个完整的圆,解决此类问题一定要画出图形,数形结合解决.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
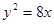 上一点P到
上一点P到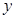 轴的距离是4,则点P到该抛物线焦点的距离是( )
轴的距离是4,则点P到该抛物线焦点的距离是( )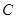 :
: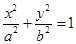 (
(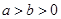 )的短轴长与焦距相等,且过定点
)的短轴长与焦距相等,且过定点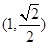 ,倾斜角为
,倾斜角为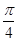 的直线
的直线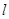 交椭圆
交椭圆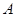 、
、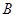 两点.
两点.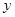 轴上截距的范围.
轴上截距的范围.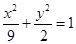 的焦点为
的焦点为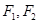 ,点
,点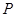 在椭圆上,若
在椭圆上,若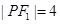 ,
,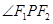
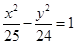 上的点
上的点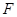 到一个焦点的距离为11,则它到另一个焦点的距离为( )
到一个焦点的距离为11,则它到另一个焦点的距离为( )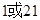
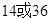
 的两个焦点,A和B是以O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则离心率为( )
的两个焦点,A和B是以O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则离心率为( )
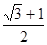



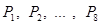 是抛物线
是抛物线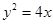 上的点,它们的横坐标依次为
上的点,它们的横坐标依次为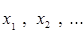
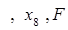 是抛物线的焦点,若
是抛物线的焦点,若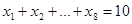 ,则
,则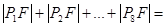 _______________.
_______________.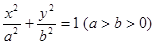 的右焦点F为
的右焦点F为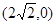 ,G上的点到点F的最大距离为
,G上的点到点F的最大距离为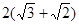 ,斜率为1的直线
,斜率为1的直线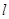 与椭圆G交与
与椭圆G交与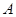 、
、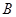 两点,以AB为底边作等腰三角形,顶点为P(-3,2)
两点,以AB为底边作等腰三角形,顶点为P(-3,2)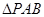 的面积。
的面积。 的焦点弦
的焦点弦 坐标分别为
坐标分别为 ,则
,则 的值一定等于( )
的值一定等于( )


