题目内容
已知向量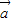 =(sin
=(sin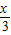 ,cos
,cos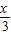 ),
),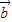 =(cos
=(cos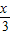 ,
,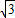 cos
cos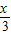 ),函数f(x)=
),函数f(x)=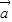 •
•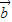 ,
,(1)求函数f(x)的单调递增区间;
(2)如果△ABC的三边a、b、c,满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
【答案】分析:(1)利用向量的数量积公式及辅助角公式,化简函数,即可求得函数f(x)的单调递增区间;
(2)通过b2=ac,利用余弦定理求出cosx的范围,然后求出x的范围,进而可求三角函数的值域.
解答:解:(1)∵向量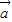 =(sin
=(sin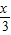 ,cos
,cos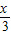 )
)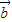 =(cos
=(cos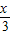 ,
,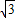 cos
cos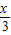 ),
),
∴函数f(x)=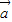 •
•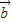 =sin(
=sin(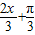 )+
)+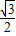 ,
,
令2kπ-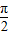 ≤
≤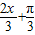 ≤2kπ+
≤2kπ+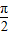 ,解得
,解得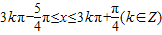 .
.
故函数f(x)的单调递增区间为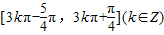 .
.
(2)由已知b2=ac,cosx=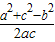 =
=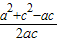 ≥
≥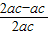 =
= ,∴
,∴ ≤cosx<1,∴0<x≤
≤cosx<1,∴0<x≤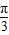
∴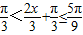
∴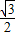 <sin(
<sin(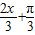 )≤1,
)≤1,
∴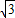 <sin(
<sin(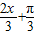 )+
)+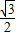 ≤1+
≤1+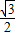
∴f(x)的值域为(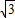 ,1+
,1+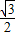 ]
]
点评:本题是中档题,考查三角函数的化简求值,余弦定理的应用,正弦函数的值域的求法,考查计算能力.
(2)通过b2=ac,利用余弦定理求出cosx的范围,然后求出x的范围,进而可求三角函数的值域.
解答:解:(1)∵向量
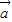 =(sin
=(sin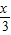 ,cos
,cos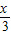 )
)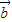 =(cos
=(cos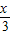 ,
,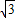 cos
cos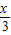 ),
),∴函数f(x)=
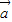 •
•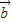 =sin(
=sin(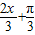 )+
)+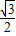 ,
,令2kπ-
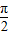 ≤
≤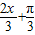 ≤2kπ+
≤2kπ+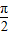 ,解得
,解得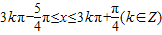 .
.故函数f(x)的单调递增区间为
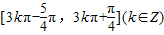 .
.(2)由已知b2=ac,cosx=
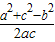 =
=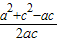 ≥
≥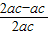 =
= ,∴
,∴ ≤cosx<1,∴0<x≤
≤cosx<1,∴0<x≤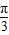
∴
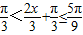
∴
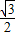 <sin(
<sin(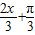 )≤1,
)≤1,∴
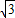 <sin(
<sin(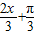 )+
)+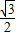 ≤1+
≤1+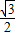
∴f(x)的值域为(
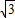 ,1+
,1+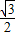 ]
]点评:本题是中档题,考查三角函数的化简求值,余弦定理的应用,正弦函数的值域的求法,考查计算能力.

练习册系列答案
相关题目