题目内容

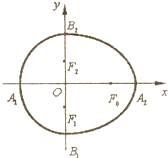
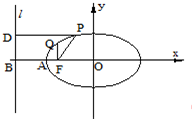
如图，已知椭圆中心在原点，F是焦点，A为顶点，准线l交x轴于点B，点P，Q在椭圆上，且PD⊥l于D，QF⊥AO，则①
|PF|
|PD|
；②
|QF|
|BF|
；③
|AO|
|BO|
；④
|AF|
|AB|
；⑤
|FO|
|AO|
，其中比值为椭圆的离心率的有（　　）
A．1个B．3个C．4个D．5个

设椭圆的方程为
x2
a2
+
y2
b2
=1，（0＜a＜b）依次分析5个比值的式子可得：
①、根据椭圆的第二定义，可得
|PF|
|PD|
=e，故符合；
②、根据椭圆的性质，可得|BF|=
a2
c
-c=
b2
c
，|QF|=
b2
a
，则
|QF|
|BF|
=
c
a
=e，故符合；
③、由椭圆的性质，可得|AO|=a，|BO|=
a2
c
，则
|AO|
|BO|
=
c
a
=e，故符合；
④、由椭圆的性质，可得|AF|=a-c，|AB|=
a2
c
-a=
a
c
（a-c），则
|AF|
|AB|
=
c
a
=e，故符合；
⑤、由椭圆的性质，可得|AO|=a，|FO|=c，
|FO|
|AO|
=
c
a
=e，故符合；
故选D．
练习册系列答案
相关题目
若方程
x2
25-k
+
y2
k-9
=1表示椭圆，则k的取值范围是（　　）
A．（9，17）B．（9，25）C．（9，17）∪（17，25）D．（-∞，9）∪（25，+∞）
已知椭圆
x2
2
+y2=1的左右焦点分别为F1，F2，若过点P（0，-2）及F1的直线交椭圆于A，B两点，求△ABF2的面积．
请阅读以下材料，然后解决问题：
①设椭圆的长半轴长为m短半轴长为b，则椭圆的面积为πab
②我们把由半椭圆C1：
y2
b2
+
x2
c2
=1（x≤0）与半椭圆C2：
x2
a2
+
y2
b2
=1（x≥0）合成的曲线称作“果圆”，其中a2=b2+c2，a＞0，b＞c＞0
如图，设点F0，F1，F2是相应椭圆的焦点，A1，A2和B1，B2是“果圆”与x，y轴的交点，若△F0F1F2是边长为1的等边三角形，则上述“果圆”的面积为：______．
过椭圆
x2
16
+
y2
9
=1的一个焦点F1的直线与椭圆交于A，B两点，则A，B与椭圆的另一个焦点F2构成△ABF2，则△ABF2的周长是______．
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)，左焦点为E，右焦点为F，上顶点为B，若△BEF为等边三角形，则此椭圆的离心率为（　　）
A．
5
+1
2
B．
5
-1
2
C．
1
2
D．2-
3
若椭圆的焦距长等于它的短轴长，则椭圆的离心率等于______．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点分别为F1，F2，P是椭圆上的一点，且|PF1|，|F1F2|，|PF2|成等比数列，则椭圆的离心率的取值范围为（　　）
A．[
1
2
，
2
2
]		B．[
5
-1，
1
2
]		C．[
2
-1，
1
2
]		D．[
5
5
，
1
2
]
设椭圆
x2
4
+
y2
3
=1的左右焦点分别为F1，F2，点P在椭圆上，若
PF1
•
PF2
=
5
2
，则|
PF1
|•|
PF2
|=（　　）
A．2B．3C．
7
2
D．
9
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网