题目内容
函数f(x)=3kx+1-2k在(-1,1)上存在x0,使f(x0)=0,则k的取值范围是( )
A、(-1,
| ||
| B、(-∞,-1) | ||
C、(-∞,-1)∪(
| ||
D、(
|
分析:根据零点存在定理,函数f(x)=3kx+1-2k在(-1,1)上存在x0,使f(x0)=0,则表示函数f(x)=3kx+1-2k在(-1,1)上存在有零点,则f(-1)•f(1)<0,由此我们可以构造一个关于a的不等式,解不等式即可得到答案.
解答:解:若函数f(x)=3kx+1-2k在(-,1)上存在x0,使f(x0)=0,
则表示函数f(x)=3kx+1-2k在(-,1)上存在零点
则f(-1)•f(1)<0
即(1-5k)•(1+k)<0
解得:a>
或a<-1
∴k的取值范围是(-∞,-1)∪(
,+∞)
故选C.
则表示函数f(x)=3kx+1-2k在(-,1)上存在零点
则f(-1)•f(1)<0
即(1-5k)•(1+k)<0
解得:a>
| 1 |
| 5 |
∴k的取值范围是(-∞,-1)∪(
| 1 |
| 5 |
故选C.
点评:本题考查的知识点是函数零点的判定定理,其中根据零点判定定理构造关于k的不等式,是解答本题的关键,属基础题.

练习册系列答案
相关题目
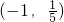
 ,+∞)
,+∞)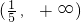

 ,+∞)
,+∞)