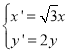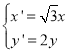Question

【题目】以双曲线上一点为圆心作圆，该圆与轴相切于的一个焦点，与轴交于两点，若，则双曲线的离心率________.

Answer 1

【答案】

【解析】

由题意可设F（c，0），MF⊥x轴，可设M（c，n），n＞0，设x＝c，代入双曲线的方程，可得M的坐标，圆的半径，运用弦长公式，可得|PQ|＝2c，可得a，c的方程，运用离心率公式计算即可得到所求值．

由题意可设F（c，0），

MF⊥x轴，可设M（c，n），n＞0，

设x＝c，代入双曲线的方程可得y＝b，

即有M（c，），

可得圆的圆心为M，半径为，

即有M到y轴的距离为c，

可得|PQ|＝2c，

化简可得3b4＝4a2c2，

由c2＝a2+b2，可得3c4﹣10c2a2+3a4＝0，

由e，可得3e4﹣10e2+3＝0，

解得e2＝3（舍去），

即有e．

故答案为：．