Question

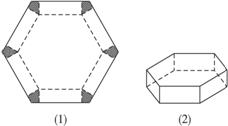
将边长为1的正六边形铁皮的六个角各切去一个全等的四边形，再沿虚线折起，做成一个无盖的正六棱柱容器．当这个正六棱柱容器的底面边长为

2

3

时，其容积最大．

Answer 1

分析：要求正六棱柱容器的容积最大，得需要得出容积表达式；由柱体的体积公式知，底面积是正六边形，是六个全等小正△的和，高是Rt△中60°角所对的直角边，由高和底面积得出容积函数，用求导法可以求出最大值时的自变量取值．

解答：解：如图，设底面六边形的边长为x，高为d，则
d=

3

•

1

2

•(1-x)；
又底面六边形的面积为：
S=6•

1

2

•x²•sin60°=

3

2

3

x2；
所以，这个正六棱柱容器的容积为：
V=Sd=

3

2

3

x2•

3

2

(1-x)=

9

4

(x2-x3)，
则对V求导，得
V′=

9

4

(2x-3x2)，令V′=0，得x=0或x=

2

3

，
当0＜x＜

2

3

时，V′＞0，V是增函数；当x＞

2

3

时，V′＜0，V是减函数；
∴x=

2

3

时，V有最大值．
故答案为：

2

3

．

点评：本题通过建立体积函数表达式，由求导的方法求函数最大值，是比较常用的解题思路，也是中学数学的重要内容．