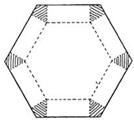
题目内容
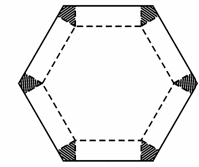
如图，将边长为1的正六边形铁皮的六个角各切去一个全等的四边形，再沿虚线折起，做成一个无盖的正六棱柱容器.当这个正六棱柱容器的底面边长为多少时，其容积最大.
解析：设被切去的全等四边形的一边长为x，如图，则正六棱柱的底面边长为1-2x,高为x,
∴正六棱柱的体积V=6×
(1-2x)2×3x(0＜x＜
),化简得V=
（4x3-4x2+x).
又V′=
（12x2-8x+1),由V′=0，得x=
或x=
.
∵当x∈(0, 
)时，V′＞0,V是增函数；
当x∈(
,
）时V′＜0，V是减函数.
∴当x=
时，V有最大值，此时正六棱柱的底面边长为
.
练习册系列答案
快捷英语周周练系列答案
相关题目
如图，将边长为1的正六边形铁皮的六个角各切去一个全等的四边形，再沿虚线折起，做成一个无盖的正六棱柱容器．当这个正六棱柱容器的底面边长为
