题目内容
如图(1)所示,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器如图(2).当这个正六棱柱容器的底面边长为______________________时,其容积最大.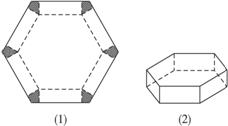
解析:设底面边长为x,则底面积S=![]() x2,高h=(1-x)sin60°=
x2,高h=(1-x)sin60°=![]() (1-x),
(1-x),
所以V=![]() x2(1-x)=
x2(1-x)=![]() (2-2x)x2≤
(2-2x)x2≤![]() (
(![]() )3=
)3=![]() .
.
当且仅当2-2x=x,即x=![]() 时等式成立,故当底面边长为
时等式成立,故当底面边长为![]() 时,其容积最大.
时,其容积最大.
答案:![]()

练习册系列答案
相关题目
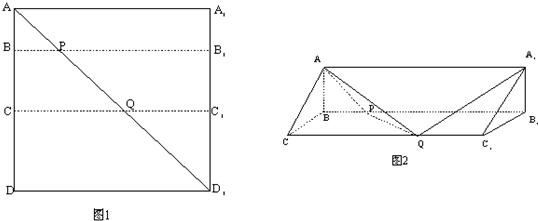
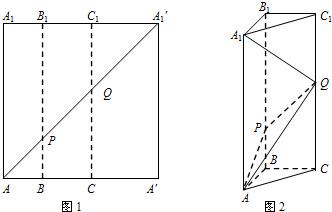 如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.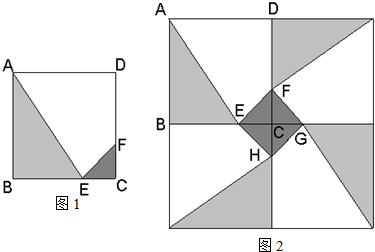
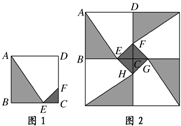 (2007•上海)某人定制了一批地砖.每块地砖 (如图1所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形EFGH.
(2007•上海)某人定制了一批地砖.每块地砖 (如图1所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形EFGH.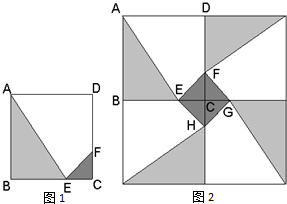 某人定制了一批地砖,每块地砖 (如图1所示)是边长为40cm的正方形ABCD,点E,F分别在边BC和CD上,△CFE,△ABE和四边形AEFD均由单一材料制成,制成△CFE,△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形EFGH.则当CE=
某人定制了一批地砖,每块地砖 (如图1所示)是边长为40cm的正方形ABCD,点E,F分别在边BC和CD上,△CFE,△ABE和四边形AEFD均由单一材料制成,制成△CFE,△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形EFGH.则当CE=