题目内容
已知直线(1+k)x+y-k-2=0恒过点P,则点P关于直线x-y-2=0的对称点的坐标是( )
| A、(3,-2) | B、(2,-3) | C、(1,-3) | D、(3,-1) |
分析:由直线(1+k)x+y-k-2=0化为k(x-1)+(x+y-2)=0,令
解得此直线恒过点P(1,1).设点P关于直线x-y-2=0的对称点为P′(m,n),利用垂直平分线的性质可得:
,解得m,n即可.
|
|
解答:解:由直线(1+k)x+y-k-2=0化为k(x-1)+(x+y-2)=0,
令
,
解得
,
于是此直线恒过点P(1,1).
设点P关于直线x-y-2=0的对称点为P′(m,n),
则
,
解得
.
∴P′(3,-1).
故选:D.
令
|
解得
|
于是此直线恒过点P(1,1).
设点P关于直线x-y-2=0的对称点为P′(m,n),
则
|
解得
|
∴P′(3,-1).
故选:D.
点评:本题考查了直线系的性质和轴对称的性质,属于基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
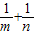 的最小值为( )
的最小值为( )

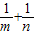 的最小值为( )
的最小值为( )
