题目内容
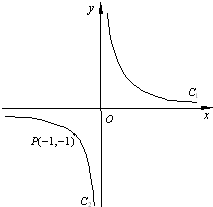 设双曲线xy=1的两支为C1,C2(如图),正三角形PQR的三顶点位于此双曲线上.
设双曲线xy=1的两支为C1,C2(如图),正三角形PQR的三顶点位于此双曲线上.(1)求证:P、Q、R不能都在双曲线的同一支上;
(2)设P(-1,-1)在C2上,Q、R在C1上,求顶点Q、R的坐标.
分析:(1)设某个正三角形的三个顶点都在同一支上,此三点坐标为P(x1,
),O(x2,
),R(x3,
),则
>
>
>0,由此导出tan∠POR<0,从而∠POR为钝角,即△POR不可能是正三角形.
(2)P(-1,-1),设O(x2,
),点P在直线y=x上,以P为圆心,|PO|为半径作圆,此圆与双曲线第一象限内的另一交点R满足|PO|=|PR|,由圆与双曲线都与y=x对称,知O与R关于y=x对称,且在第一象限内此两条曲线没有其他交点(二曲线的交点个数),于是R(
,x2),由此能够求出顶点Q、R的坐标.
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x3 |
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x3 |
(2)P(-1,-1),设O(x2,
| 1 |
| x2 |
| 1 |
| x2 |
解答:(1)证明:设某个正三角形的三个顶点都在同一支上,
此三点坐标为P(x1,
),O(x2,
),R(x3,
),
则
>
>
>0,
kPO=
=-
,kPR=
=-
,
tan∠POR=
<0,
从而∠POR为钝角,即△POR不可能是正三角形.
所以P、Q、R不能都在双曲线的同一支上.
(2)解:P(-1,-1),设O(x2,
),点P在直线y=x上,
以P为圆心,|PO|为半径作圆,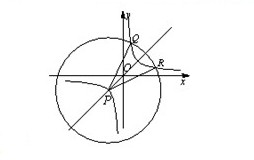
此圆与双曲线第一象限内的另一交点R满足|PO|=|PR|,
由圆与双曲线都与y=x对称,
知O与R关于y=x对称,
且在第一象限内此两条曲线没有其他交点(二曲线的交点个数),
于是R(
,x2),
∴PO与y=x的夹角等于30°,PO所在直线的倾斜角等于75°,
tan75°=
=2+
.
PO所在的直线方程为y+1=(2+
)(x+1),
代入xy=1,
解得O(2-
,2+
),于是R(2+
,2-
).
此三点坐标为P(x1,
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x3 |
则
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x3 |
kPO=
| ||||
| x2-x1 |
| 1 |
| x1x2 |
| ||||
| x3-x1 |
| 1 |
| x2x3 |
tan∠POR=
-
| ||||
1+
|
从而∠POR为钝角,即△POR不可能是正三角形.
所以P、Q、R不能都在双曲线的同一支上.
(2)解:P(-1,-1),设O(x2,
| 1 |
| x2 |
以P为圆心,|PO|为半径作圆,

此圆与双曲线第一象限内的另一交点R满足|PO|=|PR|,
由圆与双曲线都与y=x对称,
知O与R关于y=x对称,
且在第一象限内此两条曲线没有其他交点(二曲线的交点个数),
于是R(
| 1 |
| x2 |
∴PO与y=x的夹角等于30°,PO所在直线的倾斜角等于75°,
tan75°=
1+
| ||||
1-
|
| 3 |
PO所在的直线方程为y+1=(2+
| 3 |
代入xy=1,
解得O(2-
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查三点不能都在双曲线的同一支上的证明,考查双曲线顶点坐标的求法,难度大,综合性强,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目

