题目内容
设双曲线xy=1的两支C1、C2，正三角形PQR的三个顶点位于此双曲线上，求证：P、Q、R不能都在双曲线的同一支上．
<
答案：
解析：
解析：
 
因此，∠PQR是钝角，这与△PQR是正三角形相矛盾， 故P、Q、R不能都在等轴双曲线xy=1的同一支上．
由(1)(2)联立解得△PQR的垂心 当P、Q、R在双曲线的同一支如C1上时，则－x1x2x3＜0，而H在另一支C2上，即H在△PQR的外部，所以△PQR是钝角三角形，与已知条件△PQR是正三角形不符合，故，P、Q、 R不能都在双曲线的同一支上．
|
练习册系列答案
相关题目
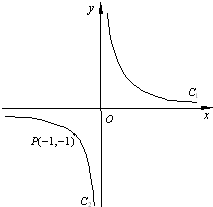设双曲线xy=1的两支为C1，C2（如图），正三角形PQR的三顶点位于此双曲线上．（1）求证：P、Q、R不能都在双曲线的同一支上；
（2）设P（-1，-1）在C2上，Q、R在C1上，求顶点Q、R的坐标．
