题目内容
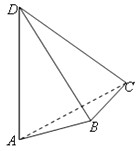 (2012•上海)如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是
(2012•上海)如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是| 2 |
| 3 |
| a2-c2-1 |
| 2 |
| 3 |
| a2-c2-1 |
分析:作BE⊥AD于E,连接CE,说明B与C都是在以AD为焦距的椭球上,且BE、CE都垂直于焦距AD,BE=CE.
取BC中点F,推出四面体ABCD的体积的最大值,当△ABD是等腰直角三角形时几何体的体积最大,求解即可.
取BC中点F,推出四面体ABCD的体积的最大值,当△ABD是等腰直角三角形时几何体的体积最大,求解即可.
解答: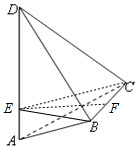 解:作BE⊥AD于E,连接CE,则AD⊥平面BEC,所以CE⊥AD,
解:作BE⊥AD于E,连接CE,则AD⊥平面BEC,所以CE⊥AD,
由题设,B与C都是在以AD为焦点的椭圆上,且BE、CE都垂直于焦距AD,
AB+BD=AC+CD=2a,显然△ABD≌△ACD,所以BE=CE.
取BC中点F,∴EF⊥BC,EF⊥AD,要求四面体ABCD的体积的最大值,因为AD是定值,只需三角形EBC的面积最大,因为BC是定值,所以只需EF最大即可,
当△ABD是等腰直角三角形时几何体的体积最大,∵AB+BD=AC+CD=2a,
∴AB=a,所以EB=
,EF=
,
所以几何体的体积为:
×2×
×2c×
=
c
.
故答案为:
c
.
 解:作BE⊥AD于E,连接CE,则AD⊥平面BEC,所以CE⊥AD,
解:作BE⊥AD于E,连接CE,则AD⊥平面BEC,所以CE⊥AD,由题设,B与C都是在以AD为焦点的椭圆上,且BE、CE都垂直于焦距AD,
AB+BD=AC+CD=2a,显然△ABD≌△ACD,所以BE=CE.
取BC中点F,∴EF⊥BC,EF⊥AD,要求四面体ABCD的体积的最大值,因为AD是定值,只需三角形EBC的面积最大,因为BC是定值,所以只需EF最大即可,
当△ABD是等腰直角三角形时几何体的体积最大,∵AB+BD=AC+CD=2a,
∴AB=a,所以EB=
| a2-c2 |
| a2-c2-1 |
所以几何体的体积为:
| 1 |
| 3 |
| a2-c2-1 |
| 1 |
| 2 |
| 2 |
| 3 |
| a2-c2-1 |
故答案为:
| 2 |
| 3 |
| a2-c2-1 |
点评:本题考查棱柱、棱锥、棱台的体积,考查空间想象能力,逻辑推理能力以及计算能力.

练习册系列答案
相关题目
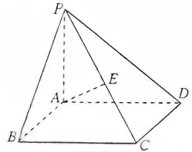 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2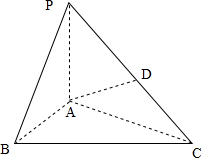 (2012•上海)如图,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点,已知∠BAC=
(2012•上海)如图,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点,已知∠BAC=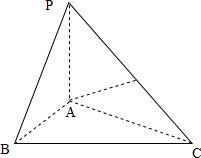
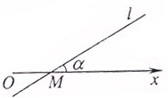 (2012•上海)如图,在极坐标系中,过点M(2,0)的直线l与极轴的夹角a=
(2012•上海)如图,在极坐标系中,过点M(2,0)的直线l与极轴的夹角a=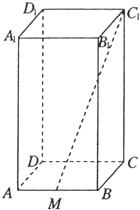 (2012•上海)如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,高为2,M为线段AB的中点.
(2012•上海)如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,高为2,M为线段AB的中点.