题目内容
已知向量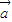 =(sin(ωx+ϕ),2),
=(sin(ωx+ϕ),2),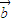 =(1,cos(ωx+ϕ))
=(1,cos(ωx+ϕ))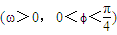 ,函数f(x)=(
,函数f(x)=(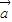 +
+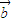 )•(
)•(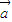 -
-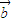 )的图象过点
)的图象过点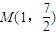 ,且该函数相邻两条对称轴间的距离为2.
,且该函数相邻两条对称轴间的距离为2.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)将函数y=f(x)图象按向量
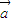 =
=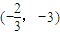 平移后,得到函数y=g(x)的图象,讨论函数y=g(x)在区间[1,2]上的单调性.
平移后,得到函数y=g(x)的图象,讨论函数y=g(x)在区间[1,2]上的单调性.
【答案】分析:(Ⅰ)通过函数f(x)=(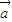 +
+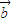 )•(
)•(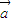 -
-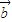 )利用向量的数量积,结合三角函数的二倍角公式化简函数的表达式,利用周期求出ω,图象通过点,求出ϕ,得到函数f(x)的解析式;
)利用向量的数量积,结合三角函数的二倍角公式化简函数的表达式,利用周期求出ω,图象通过点,求出ϕ,得到函数f(x)的解析式;
(Ⅱ)将函数y=f(x)图象按向量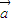 =
=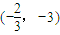 平移后,得到函数y=g(x)的图象,得到函数的解析式,根据[1,2]求出函数的单调性.
平移后,得到函数y=g(x)的图象,得到函数的解析式,根据[1,2]求出函数的单调性.
解答:解:(Ⅰ)f(x)=(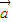 +
+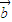 )•(
)•(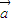 -
-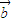 )=
)= 2-
2-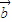 2=|
2=|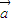 |2-|
|2-|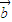 |2=sin2(ωx+ϕ)+4-cos2(ωx+ϕ)-1=3-cos(2ωx+2ϕ).
|2=sin2(ωx+ϕ)+4-cos2(ωx+ϕ)-1=3-cos(2ωx+2ϕ).
∴f(x)的最小正周期为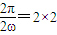 ,即
,即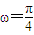 .
.
又f(x)的图象过点M(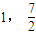 ),
),
∴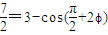 ,即
,即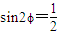 .
.
而 ,∴
,∴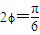 ,则
,则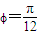 .
.
∴f(x)=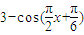 ..…(6分)
..…(6分)
(Ⅱ)依题意,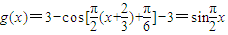 .
.
∵x∈[1,2],∴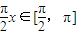 .
.
∴函数y=g(x)在[1,2]上单调递减.…(12分)
点评:本题是中档题,通过向量的数量积,三角函数的公式的应用,函数图象的特点求出函数的解析式是解题的关键,注意角的范围,考查计算能力.
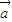 +
+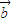 )•(
)•(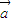 -
-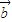 )利用向量的数量积,结合三角函数的二倍角公式化简函数的表达式,利用周期求出ω,图象通过点,求出ϕ,得到函数f(x)的解析式;
)利用向量的数量积,结合三角函数的二倍角公式化简函数的表达式,利用周期求出ω,图象通过点,求出ϕ,得到函数f(x)的解析式;(Ⅱ)将函数y=f(x)图象按向量
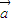 =
=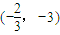 平移后,得到函数y=g(x)的图象,得到函数的解析式,根据[1,2]求出函数的单调性.
平移后,得到函数y=g(x)的图象,得到函数的解析式,根据[1,2]求出函数的单调性.解答:解:(Ⅰ)f(x)=(
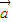 +
+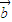 )•(
)•(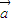 -
-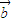 )=
)= 2-
2-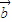 2=|
2=|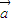 |2-|
|2-|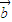 |2=sin2(ωx+ϕ)+4-cos2(ωx+ϕ)-1=3-cos(2ωx+2ϕ).
|2=sin2(ωx+ϕ)+4-cos2(ωx+ϕ)-1=3-cos(2ωx+2ϕ).∴f(x)的最小正周期为
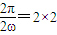 ,即
,即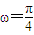 .
.又f(x)的图象过点M(
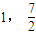 ),
),∴
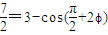 ,即
,即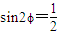 .
.而
 ,∴
,∴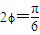 ,则
,则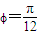 .
.∴f(x)=
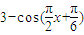 ..…(6分)
..…(6分)(Ⅱ)依题意,
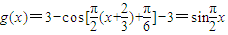 .
.∵x∈[1,2],∴
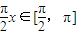 .
.∴函数y=g(x)在[1,2]上单调递减.…(12分)
点评:本题是中档题,通过向量的数量积,三角函数的公式的应用,函数图象的特点求出函数的解析式是解题的关键,注意角的范围,考查计算能力.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目