题目内容
9. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的长轴长是短轴长的两倍,焦距为2$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的长轴长是短轴长的两倍,焦距为2$\sqrt{3}$.(1)求椭圆C的标准方程;
(2)设A、B是四条直线x=±a,y=±b所围成的两个顶点,P是椭圆C上的任意一点,若$\overrightarrow{OP}=m\overrightarrow{OA}+n\overrightarrow{OB}$,求证:动点Q(m,n)在定圆上运动.
分析 (1)由椭圆的长轴长是短轴长的两倍,焦距为2$\sqrt{3}$,列出方程组,能求出椭圆方程.
(2)由已得A(2,1),B(-2,1),设P(x0,y0),由此能证明点Q(m,n)在定圆x2+y2=$\frac{1}{2}$运动.
解答 (1)解:∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的长轴长是短轴长的两倍,焦距为2$\sqrt{3}$,
∴$\left\{\begin{array}{l}{a=2b}\\{2c=2\sqrt{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=1,c=$\sqrt{3}$,
∴椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(2)证明:∵A、B是四条直线x=±2,y=±1所围成的两个顶点,
∴A(2,1),B(-2,1),设P(x0,y0),
则$\frac{{{x}_{0}}^{2}}{4}$+y02=1.由$\overrightarrow{OP}=m\overrightarrow{OA}+n\overrightarrow{OB}$,得$\left\{\begin{array}{l}{{x}_{0}=2(m-n)}\\{{y}_{0}=m+n}\end{array}\right.$,
∴$\frac{4(m-n)^{2}}{4}$+(m+n)2=1,故点Q(m,n)在定圆x2+y2=$\frac{1}{2}$运动.
点评 本题考查椭圆的方程的求法,考查动点在定圆上运动的证明,解题时要认真审题,注意椭圆性质的应用,考查转化思想计算能力.

练习册系列答案
相关题目
19.设F1、F2是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+${\frac{{y}^{2}}{{b}^{2}}}^{\;}$=1(a>b>0)的左右焦点,P为直线x=$\frac{5a}{4}$上一点,△F2PF1是底角为30°的等腰三角形,则椭圆C的离心率为( )
| A. | $\frac{5}{8}$ | B. | $\frac{\sqrt{10}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
4.已知A,B分别为椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,不同两点P,Q在椭圆C上,且关于x轴对称,设直线AP,BQ的斜率分别为m,n,则当$\frac{2b}{a}+\frac{a}{b}+\frac{1}{2mn}$+ln|m|+ln|n|取最小值时,椭圆C的离心率为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
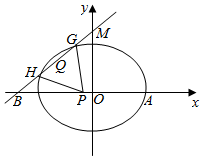 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点A(2,0),离心率$e=\frac{1}{2}$,斜率为k(0<k≤1)直线l过点M(0,2),与椭圆C交于G,H两点(G在M,H之间),与x轴交于点B.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点A(2,0),离心率$e=\frac{1}{2}$,斜率为k(0<k≤1)直线l过点M(0,2),与椭圆C交于G,H两点(G在M,H之间),与x轴交于点B. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点到直线x-y+3$\sqrt{2}$=0的距离为5,且椭圆的一个长轴端点与一个短轴端点间的距离为$\sqrt{10}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点到直线x-y+3$\sqrt{2}$=0的距离为5,且椭圆的一个长轴端点与一个短轴端点间的距离为$\sqrt{10}$.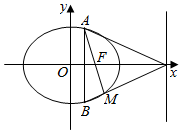 如图,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,F为该椭圆的右焦点,若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M(x0,y0).
如图,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,F为该椭圆的右焦点,若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M(x0,y0).
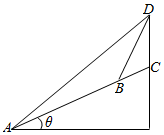 如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.
如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.