题目内容
设a,b均为正数,(Ⅰ)求证:
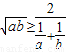 ;
;(Ⅱ)如果依次称
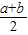 、
、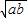 、
、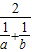 分别为a,b两数的算术平均数、几何平均数、调和平均数.如右图,C为线段AB上的点,令AC=a,CB=b,O为AB的垂线交半圆于D.连结OD,AD,BD.过点C作OD的垂线,垂足为E.图中线段OD的长度是a,b的算术平均数,请分别用图中线段的长度来表示a,b两数的几何平均数和调和平均数,并说明理由.
分别为a,b两数的算术平均数、几何平均数、调和平均数.如右图,C为线段AB上的点,令AC=a,CB=b,O为AB的垂线交半圆于D.连结OD,AD,BD.过点C作OD的垂线,垂足为E.图中线段OD的长度是a,b的算术平均数,请分别用图中线段的长度来表示a,b两数的几何平均数和调和平均数,并说明理由.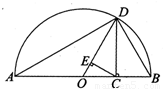
【答案】分析:(I)由于a,b均为正数,根据基本不等式,可得
 =
= ,即可得出
,即可得出 ;
;
(II)在直角三角形中,由DC为高,根据射影定理可得CD2=AC•CB,变形两边开方,得到CD长度为a,b的几何平均数;根据在直角三角形OCD中,由射影定理可得CD2=DE•CB,得到DE的长,再由DC≥DE,得到结果.
解答:解:(I)证明:由于a,b均为正数,根据基本不等式,可得
 =
= ,即
,即 ,
,
当且仅当a=b时,等号成立.
(II)在Rt△ADB中DC为高,则由射影定理可得CD2=AC•CB,
∴CD= ,即CD长度为a,b的几何平均数,
,即CD长度为a,b的几何平均数,
在直角三角形OCD中,由射影定理可得CD2=DE•CB,
∴DE= =
= =
= ,由DC≥DE,得
,由DC≥DE,得 ≥
≥ ,当且仅当a=b时,等号成立,
,当且仅当a=b时,等号成立,
∴线段DE的长度分别为a,b的调和平均数.
点评:本题是一个新定义问题,解题过程中主要应用直角三角形边之间的比例关系,得到比例式,本题是一个平面几何与代数中的平均数结合的问题,是一个综合题.

 =
= ,即可得出
,即可得出 ;
;(II)在直角三角形中,由DC为高,根据射影定理可得CD2=AC•CB,变形两边开方,得到CD长度为a,b的几何平均数;根据在直角三角形OCD中,由射影定理可得CD2=DE•CB,得到DE的长,再由DC≥DE,得到结果.
解答:解:(I)证明:由于a,b均为正数,根据基本不等式,可得

 =
= ,即
,即 ,
,当且仅当a=b时,等号成立.
(II)在Rt△ADB中DC为高,则由射影定理可得CD2=AC•CB,
∴CD=
 ,即CD长度为a,b的几何平均数,
,即CD长度为a,b的几何平均数,在直角三角形OCD中,由射影定理可得CD2=DE•CB,
∴DE=
 =
= =
= ,由DC≥DE,得
,由DC≥DE,得 ≥
≥ ,当且仅当a=b时,等号成立,
,当且仅当a=b时,等号成立,∴线段DE的长度分别为a,b的调和平均数.
点评:本题是一个新定义问题,解题过程中主要应用直角三角形边之间的比例关系,得到比例式,本题是一个平面几何与代数中的平均数结合的问题,是一个综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
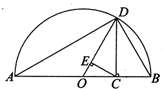 设a,b均为正数,
设a,b均为正数,