题目内容
4.设直线l:y=kx+1经过抛物线x2=2py(p>0)的焦点F,则p=2;已知Q,M分别是抛物线及其准线上的点,若$\overrightarrow{MQ}$=2$\overrightarrow{QF}$,则|MF|=4.分析 由直线方程求出直线所过定点的坐标,从而得到抛物线的焦点坐标,则p可求;作出抛物线图形,数形结合得到|MF|=2p,则答案可求.
解答 解:∵直线l:y=kx+1过定点(0,1),即抛物线x2=2py(p>0)的焦点F为(0,1),
∴$\frac{p}{2}=1$,则p=2;
则抛物线方程为x2=4y,如图,
∵$\overrightarrow{MQ}$=2$\overrightarrow{QF}$,
∴|MQ|=2|QE|,则∠EMQ=30°,
∴|MF|=2p=4.
故答案为:2;4.
点评 本题考查了抛物线的简单性质,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
17.设复数z=1+i(i是虚数单位),则$\frac{2}{z}$=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
12.已知函数f(x)=-2x-1+$\frac{1}{{{2^{x+1}}}}$,g(x)=x3-3x,那么函数y=f(g(x))是( )
| A. | 奇函数,且在(0,1)上是增函数,在(1,+∞)上是减函数 | |
| B. | 奇函数,且在(0,1)上是减函数,在(1,+∞)上是增函数 | |
| C. | 偶函数,且在(0,1)上是增函数,在(1,+∞)上是减函数 | |
| D. | 偶函数,且在(0,1)上是减函数,在(1,+∞)上是增函数 |
 已知一个锥体的主视图和左视图如图所示,下列选项中,不可能是该锥体的俯视图的是( )
已知一个锥体的主视图和左视图如图所示,下列选项中,不可能是该锥体的俯视图的是( )



 的离心率为
的离心率为 ,以
,以 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线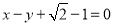 相切.
相切. 的标准方程;
的标准方程; ,和面内一点
,和面内一点 ,过点
,过点 任作直线
任作直线 与椭圆
与椭圆 相交于
相交于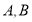 两点,设直线
两点,设直线 的斜率分别为
的斜率分别为 ,若
,若 ,试求
,试求 满足的关系式.
满足的关系式.