题目内容
已知:A(cosx,sinx),B(1,1),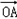 +
+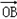 =
=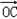 ,f(x)=
,f(x)=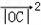 .
.
(Ⅰ)求f(x)的对称轴和对称中心;
(Ⅱ)求f(x)的单调递增区间.
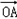 +
+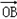 =
=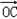 ,f(x)=
,f(x)=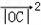 .
.(Ⅰ)求f(x)的对称轴和对称中心;
(Ⅱ)求f(x)的单调递增区间.
解:(Ⅰ).由题设知,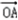 =(cosx,sinx),
=(cosx,sinx),
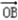 =(1,1),则
=(1,1),则 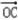 =
= +
+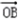 =(1+cosx,1+sinx).
=(1+cosx,1+sinx).
∴f(x)=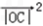 =(1+cosx)2+(1+sinx)2=3+2(sinx+cosx)=3+2
=(1+cosx)2+(1+sinx)2=3+2(sinx+cosx)=3+2 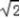 sin(x+
sin(x+ 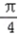 ).
).
由x+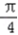 =kπ+
=kπ+ 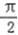 ,k∈z,即对称轴是 x=kπ+
,k∈z,即对称轴是 x=kπ+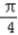 ,k∈z.
,k∈z.
对称中心横坐标满足x+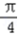 =kπ,k∈z,即 x=kπ﹣
=kπ,k∈z,即 x=kπ﹣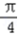 ,k∈z,
,k∈z,
故对称中心是(kπ﹣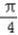 ,3),k∈z.
,3),k∈z.
(Ⅱ)当2kπ﹣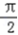 ≤x+
≤x+ 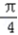 ≤2kπ+
≤2kπ+ 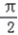 ,k∈z时,f(x)单调递增,
,k∈z时,f(x)单调递增,
即 2kπ﹣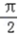 ≤x≤2kπ+
≤x≤2kπ+ 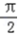 ,k∈z,
,k∈z,
∴f(x)的单增区间是[2kπ﹣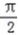 ,2kπ+
,2kπ+ 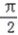 ],k∈z.
],k∈z.
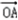 =(cosx,sinx),
=(cosx,sinx),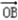 =(1,1),则
=(1,1),则 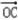 =
= +
+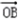 =(1+cosx,1+sinx).
=(1+cosx,1+sinx).∴f(x)=
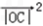 =(1+cosx)2+(1+sinx)2=3+2(sinx+cosx)=3+2
=(1+cosx)2+(1+sinx)2=3+2(sinx+cosx)=3+2 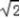 sin(x+
sin(x+ 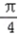 ).
).由x+
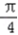 =kπ+
=kπ+ 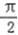 ,k∈z,即对称轴是 x=kπ+
,k∈z,即对称轴是 x=kπ+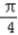 ,k∈z.
,k∈z.对称中心横坐标满足x+
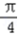 =kπ,k∈z,即 x=kπ﹣
=kπ,k∈z,即 x=kπ﹣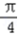 ,k∈z,
,k∈z,故对称中心是(kπ﹣
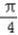 ,3),k∈z.
,3),k∈z.(Ⅱ)当2kπ﹣
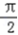 ≤x+
≤x+ 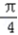 ≤2kπ+
≤2kπ+ 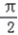 ,k∈z时,f(x)单调递增,
,k∈z时,f(x)单调递增,即 2kπ﹣
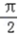 ≤x≤2kπ+
≤x≤2kπ+ 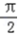 ,k∈z,
,k∈z,∴f(x)的单增区间是[2kπ﹣
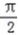 ,2kπ+
,2kπ+ 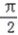 ],k∈z.
],k∈z. 
练习册系列答案
相关题目