题目内容
在一个表面积为π的球内挖去一个最大的正方体，则所剩下的几何体的体积是（ ）
分析：求出球的半径，然后求出最大的正方体的棱长，
解答：解：一个表面积为π的球，球的半径为：r=
，正方体的对角线的长为：1，
所以正方体的棱长为：
，
所以所剩下的几何体的体积是：
πr3-(
)3=
-
．
故选C．
| 1 |
| 2 |
所以正方体的棱长为：
| ||
| 3 |
所以所剩下的几何体的体积是：
| 4 |
| 3 |
| ||
| 3 |
| π |
| 6 |
| ||
| 9 |
故选C．
点评：本题是基础题，考查球的内接正方体的体积的求法，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
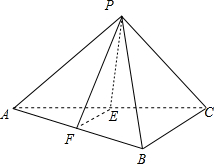已知三棱锥P-ABC中，E、F分别是AC、AB的中点，△ABC，△PEF都是正三角形，PF⊥AB．
