题目内容
如图,△ABC中,已知A(3,-1),∠B的内角平分线BD所在直线的方程是x-3y+6=0,AB上中线CE所在直线的方程是x+y-8=0,求顶点B的坐标和BC边所在直线的方程.
思路分析:如图,E是AB的中点,可设B(x1,y1),则可用B点的坐标x1、y1表示出E点的坐标,利用E点在中线x+y-8=0上可列出一个方程,再利用B点在角平分线x-3y+6=0上,再列出另一个方程,解这个方程组可得B点坐标.利用∠ABD=∠DBC,可求出BC的斜率,再用点斜式可求出BC的方程.
解:设B(x1,y1),
∵E为AB的中点,∴E(![]() ).
).
由点B在直线BD上,及E点在中线CE上,
得
∴B点的坐标为(9,5).
设BC所在直线的斜率为k,kAB=1,kBD=![]() ,
,
∵∠ABD=∠DBC,
∴tan∠ABD=tan∠DBC,
即![]() =
=![]() ,
,
即 .
.
解之,得k=-![]() .
.
∴lBC:y-5=-![]() (x-9),
(x-9),
即x+7y-44=0.

练习册系列答案
相关题目
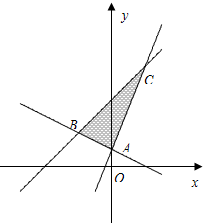 如图△ABC中,A(0,1),B(-2,2),C(2,6).
如图△ABC中,A(0,1),B(-2,2),C(2,6).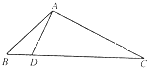 如图△ABC中,已知点D在BC边上,满足
如图△ABC中,已知点D在BC边上,满足
 如图△ABC中,A(0,1),B(-2,2),C(2,6).
如图△ABC中,A(0,1),B(-2,2),C(2,6).