题目内容
已知向量 ; 令
; 令 ,
,(1)求f(x)解析式及单调递增区间;
(2)若
 ,求函数f(x)的最大值和最小值;
,求函数f(x)的最大值和最小值;(3)若f(x)=
 ,求
,求 的值.
的值.
【答案】分析:(1)由向量 ,知
,知 =
=
= +
+ +2[
+2[ ],由此能求出f(x)解析式及单调递增区间.
],由此能求出f(x)解析式及单调递增区间.
(2)由f(x)=2+2cos(x+ ),
), ,知
,知 ,由此能求出f(x)=2+2cos(x+
,由此能求出f(x)=2+2cos(x+ )的最大值和最小值.
)的最大值和最小值.
(3)由f(x)= ,知
,知 ,由此能够求出
,由此能够求出 的值.
的值.
解答:解:(1)∵向量 ,
,
∴ =
=
= +
+ +2[
+2[ ]
]
=2+2cos(x+ ),
),
增区间是:-π+2kπ ,k∈Z,
,k∈Z,
∴ ,k∈Z,
,k∈Z,
∴f(x)解析式为f(x)=2+2cos(x+ ),
),
单调递增区间是[- ,-
,- ],k∈Z.
],k∈Z.
(2)∵f(x)=2+2cos(x+ ),
), ,
,
∴ ,
,
∴当 时,f(x)=2+2cos(x+
时,f(x)=2+2cos(x+ )有最大值2+
)有最大值2+ ;
;
当 时,f(x)=2+2cos(x+
时,f(x)=2+2cos(x+ )有最小值2-
)有最小值2- .
.
(3)∵f(x)= ,∴
,∴ ,
,
所以 .
.
点评:本题考查平面向量的综合应用,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意三角函数恒等式的灵活运用,合理地进行等价转化.
 ,知
,知 =
=
=
 +
+ +2[
+2[ ],由此能求出f(x)解析式及单调递增区间.
],由此能求出f(x)解析式及单调递增区间.(2)由f(x)=2+2cos(x+
 ),
), ,知
,知 ,由此能求出f(x)=2+2cos(x+
,由此能求出f(x)=2+2cos(x+ )的最大值和最小值.
)的最大值和最小值.(3)由f(x)=
 ,知
,知 ,由此能够求出
,由此能够求出 的值.
的值.解答:解:(1)∵向量
 ,
,∴
 =
=
=
 +
+ +2[
+2[ ]
]=2+2cos(x+
 ),
),增区间是:-π+2kπ
 ,k∈Z,
,k∈Z,∴
 ,k∈Z,
,k∈Z,∴f(x)解析式为f(x)=2+2cos(x+
 ),
),单调递增区间是[-
 ,-
,- ],k∈Z.
],k∈Z.(2)∵f(x)=2+2cos(x+
 ),
), ,
,∴
 ,
,∴当
 时,f(x)=2+2cos(x+
时,f(x)=2+2cos(x+ )有最大值2+
)有最大值2+ ;
;当
 时,f(x)=2+2cos(x+
时,f(x)=2+2cos(x+ )有最小值2-
)有最小值2- .
.(3)∵f(x)=
 ,∴
,∴ ,
,所以
 .
.点评:本题考查平面向量的综合应用,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意三角函数恒等式的灵活运用,合理地进行等价转化.

练习册系列答案
相关题目
 ; 令
; 令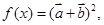
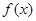 最小正周期T及单调递增区间;
最小正周期T及单调递增区间;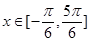 ,求函数
,求函数 ,令f(x)=
,令f(x)= .
. 时,求f(x)的值域;
时,求f(x)的值域; ,求
,求 的值.
的值.