题目内容
设数列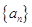 的前n项和为
的前n项和为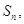 已知
已知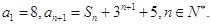
(Ⅰ)设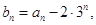 证明:数列
证明:数列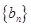 是等比数列;
是等比数列;
(Ⅱ)证明: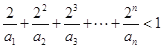 .
.
(Ⅰ)要证明 是等比数列,依据等比数列定义需证明
是等比数列,依据等比数列定义需证明 非零常数且
非零常数且


 数列
数列 是以2为首项,公比为2的等比数列。
是以2为首项,公比为2的等比数列。
(Ⅱ)由(Ⅰ)知



=
解析试题分析:(Ⅰ)

 2分
2分
当 时,
时, 5分
5分
又
 数列
数列 是以2为首项,公比为2的等比数列。… 6分
是以2为首项,公比为2的等比数列。… 6分
(Ⅱ)由(Ⅰ)知

 9分
9分
= …………12分
…………12分
考点:等比数列判定及求和
点评:判定数列是等比数列需满足相邻两项的比值是常数且首项不为0,第二问数列求和通过对通项公式的放缩转化为等比数列,套用相应的求和公式化简

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
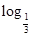 (Sn+1),求数列{bnan}的前n项和Tn.
(Sn+1),求数列{bnan}的前n项和Tn.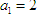 ,点
,点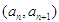 在函数
在函数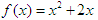 的图象上,其中
的图象上,其中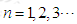
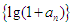 是等比数列,并求数列
是等比数列,并求数列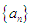 的通项公式;
的通项公式; ,求数列
,求数列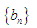 的前
的前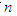 项和
项和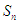 .
.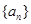 的前
的前 项和为
项和为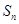 ,且满足
,且满足 .
.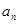 与
与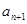 两项之间插入
两项之间插入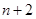 个数构成等差数列,其公差为
个数构成等差数列,其公差为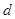 ,求数列
,求数列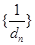 的前
的前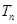 .
.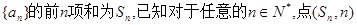 都在函数
都在函数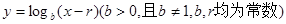 的图象上。
的图象上。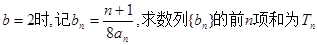 ;
;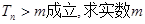 的取值范围。
的取值范围。 的各项都是正数,前
的各项都是正数,前 项和是
项和是 ,且点
,且点 在函数
在函数 的图像上.
的图像上. ,求
,求 .
.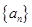 的首项
的首项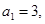 前
前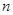 项和为
项和为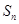 ,且
,且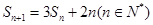 ,
,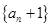 是否成等比数列?并求出数列
是否成等比数列?并求出数列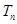 为数列
为数列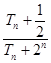 的最小值.
的最小值.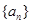 的前
的前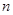 项和为
项和为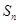 ,且
,且 ,
,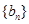 满足
满足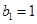 ,且点
,且点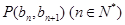 在直线
在直线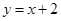 上.
上.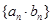 的前
的前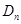 ;
;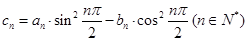 ,求数列
,求数列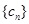 的前
的前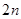 项和
项和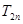 .
.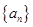 的前n项和为
的前n项和为 ,且满足
,且满足 ,n=1,2,3,…….
,n=1,2,3,……. 满足
满足 ,且
,且 ,求数列
,求数列 ,求数列
,求数列 的前n项和
的前n项和 .
.