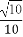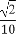题目内容
设a>0,f(x)=ax2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为[0,
],则点P到曲线y=f(x)的对称轴的距离的取值范围为 .
[0,
]
【解析】∵y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为[0,
],∴0≤f'(x0)≤1,即0≤2ax0+b≤1.又∵a>0,
∴-
≤x0≤
,∴0≤x0+≤,即点P到曲线y=f(x)的对称轴的距离的取值范围为[0,].
练习册系列答案
相关题目
在某条件下的汽车测试中,驾驶员在一次加满油后的连续行驶过程中从汽车仪表盘得到如下信息:
时间 | 油耗(升/100千米) | 可继续行驶距离(千米) |
10:00 | 9.5 | 300 |
11:00 | 9.6 | 220 |
注:油耗=
,可继续行驶距离=
;
平均油耗=
.
从以上信息可以推断在10:00-11:00这一小时内 (填上所有正确判断的序号).
①行驶了80千米;
②行驶不足80千米;
③平均油耗超过9.6升/100千米;
④平均油耗恰为9.6升/100千米;
⑤平均车速超过80千米/小时.
